Extending Mosaic Displays: Marginal, Partial, and Conditional Views of Categorical Data^*

Michael Friendly
York University

Paper, in PDF format

Slides, in PDF format

Abstract

This paper first illustrates the use of mosaic displays and other graphical methods for the analysis of multiway contingency tables. We then introduce several extensions of mosaic displays designed to integrate graphical methods for categorical data with those used for quantitative data.

For example, the scatterplot matrix shows all pairwise (marginal) views of a set of variables in a coherent display. One analog for categorical data is a matrix of mosaic displays showing some aspect of the bivariate relation between all pairs of variables. The simplest case shows the marginal relation for each pair of variables. Another case shows the conditional relation between each pair, with all other variables partialled out. For quantitative data this represents (a) a visualization of the conditional independence relations studied by graphical models. and (b) a generalization of partial residual plots.

The conditioning plot, or coplot shows a collection of (conditional) views of several variables, conditioned by the values of one or more other variables. A direct analog of the coplot for categorical data is an array of mosaic plots of the dependence among two or more variables, conditioned (or stratified) by the values of one or more given variables. Each such panel then shows the partial associations among the foreground variables; the collection of such plots show how these associations change as the given variables vary.

Key words: categorical data, conditional independence, coplots, correspondence analysis, graphical models, log-linear models, scatterplot matrix

1  Introduction

For some time I have been working on graphical methods for categorical data which aim to be comparable in scope to those available for quantitative data, including exploratory methods, and plots for model-based methods. In this paper I first illustrate the use of mosaic displays and other graphical methods for the analysis of several multiway contingency tables. Second, I introduce several extensions of mosaic displays designed to integrate graphical methods for categorical data with those used for quantitative data.

One essential difference between quantitative data and categorical data lies in the nature of the natural visual representation [ Friendly1995, Friendly1997]. For quantitative, magnitude can be represented by length (in a bar chart) or by position along a scale (dotplots, scatterplots). When the data are categorical, design principles of perception, detection, and comparison [ Friendly1998] suggest that frequencies are most usefully represented as areas.

One final introductory point: the graphics shown here are, of necessity, static graphs, designed to show both the data and some model-based analysis. Their ultimate use will, I believe, be most productive as interactive graphics tightly coupled with the model-building methods themselves. One needs to design good widgets first, however, before learning how to employ them most effectively.

2  Fourfold Display

One specialized graphical method using area as the visual mapping of cell frequency is the ``fourfold display'' ( Friendly1994 a, 1994 c; Fienberg1975 ) designed for the display of 2 ×2 (or 2×2 ×k) tables. In this display the frequency n_ij in each cell of a fourfold table is shown by a quarter circle, whose radius is proportional to Ö{ n_ij }, so the area is proportional to the cell count.

For a single 2 ×2 table the fourfold display described here also shows the frequencies by area, but scaled to depict the sample odds ratio, q = (n₁₁ n₂₂ ) /( n₁₂ n₂₁ ). An association between the variables (q ¹ 1) is shown by the tendency of diagonally opposite cells in one direction to differ in size from those in the opposite direction, and the display uses color or shading to show this direction. Confidence rings for the observed q allow a visual test of the hypothesis H₀ : q = 1. They have the property that the rings for adjacent quadrants overlap iff the observed counts are consistent with the null hypothesis.

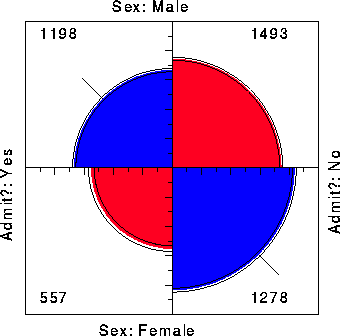
To illustrate, Figure 1 shows aggregate data on applicants to graduate school at Berkeley for the six largest departments in 1973 classified by admission and sex. At issue is whether the data show evidence of sex bias in admission practices [ Bickel et al.1975]. The figure shows the observed cell frequencies numerically in the corners of the display. Thus, there were 2691 male applicants, of whom 1193 (44.4%) were admitted, compared with 1855 female applicants of whom 557 (30.0%) were admitted. Hence the sample odds ratio, Odds (Admit|Male) / (Admit|Female) is 1.84 indicating that males were almost twice as likely to be admitted.

Figure 1: Four-fold display for Berkeley admissions: Evidence for sex bias? The area of each shaded quadrant shows the frequency, standardized to equate the margins for sex and admission. Circular arcs show the limits of a 99% confidence interval for the odds ratio.

The frequencies displayed graphically by shaded quadrants in Figure 1 are not the raw frequencies. Instead, they have been standardized (by iterative proportional fitting) so that all table margins are equal, while preserving the odds ratio. Each quarter circle is then drawn to have an area proportional to this standardized cell frequency. This makes it easier to see the association between admission and sex without being influenced by the overall admission rate or the differential tendency of males and females to apply. With this standardization the four quadrants will align when the odds ratio is 1, regardless of the marginal frequencies.

The shaded quadrants in Figure 1 do not align and the 99% confidence rings around each quadrant do not overlap, indicating that the odds ratio differs significantly from 1 --- putative evidence of gender bias. The width of the confidence rings gives a visual indication of the precision of the data-if we stopped here, we might feel quite confident of this conclusion.

2.1  Multiple strata

For example, the admissions data shown in Figure 1 were aggregated over a sample of six departments; Figure 2 displays the data for each department. The departments are labelled so that the overall acceptance rate is highest for Department A and decreases to Department F. Again each panel is standardized to equate the marginals for sex and admission. This standardization also equates for the differential total applicants across departments, facilitating visual comparison.

Figure 2: Fourfold display of Berkeley admissions, by department. In each panel the confidence rings for adjacent quadrants overlap if the odds ratio for admission and sex does not differ significantly from 1. The data in each panel have been standardized as in Figure 1.

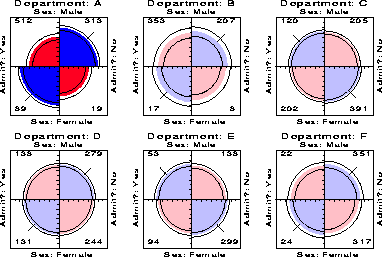
Surprisingly, Figure 2 shows that, for five of the six departments, the odds of admission is essentially identical for men and women applicants. Department A appears to differs from the others, with women approximately 2.86 ( = ( 313/19 ) /(512/89)) times more likely to gain admission. This appearance is confirmed by the confidence rings, which are joint 99% intervals for q_c in Figure 2.

This result, which contradicts the display for the aggregate data in Figure 1, is a nice example of Simpson's paradox. The resolution of this contradiction can be found in the large differences in admission rates among departments. Men and women apply to different departments differentially, and in these data women apply in larger numbers to departments that have a low acceptance rate. The aggregate results are misleading because they falsely assume men and women are equally likely to apply in each field.¹

2.2  Visualization principles

Another principle is visual impact-we want the important features of the display to be easily distinguished from the less important [ Tukey1993]. In Figure 2 distinguishes the one department for which the odds ratio differs significantly from 1 by shading intensity, even though the same information can be found by inspection of the confidence rings.

3  Mosaic displays

The construction of the mosaic is easily understood as a straightforward application of conditional probabilities. For a two-way table, with cell frequencies n_ij, and cell probabilities p_ij = n_ij / n₊₊, a unit square is first divided into rectangles whose width is proportional to the marginal frequencies n_i+, and hence to the marginal probabilities p_i = n_i+ / n₊₊. Each such rectangle is then subdivided horizontally in proportion to the conditional probabilities of the second variable given the first, p_j|i = n_ij / n_i+. Hence the area of each tile is proportional to the observed cell frequency and probability,

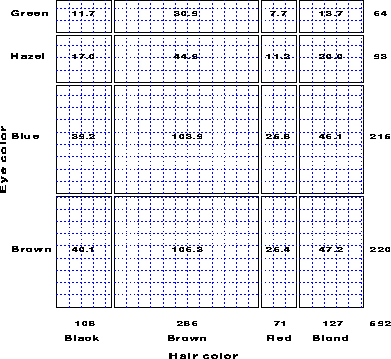
For example, Table 1 shows data on the relation between hair color and eye color among 592 subjects (students in a statistics course) collected by Snee . The Pearson c² for these data is 138.3 with 9 df, indicating substantial departure from independence.

The basic two-way mosaic for these data, shown in Figure 3, is then similar to a divided bar chart. If hair color and eye color were independent, p_ij = p_i ×p_j, and then the tiles in each row would all align. This is shown in Figure 4, which shows a mosaic constructed from the expected frequencies m_ij = n_i+ n_+j / n₊₊, under independence.

Figure 3: Basic mosaic display for hair-color and eye color data. The area of each rectangle is proportional to the observed frequency in that cell.

Figure 4: Expected frequencies under independence. The tiles align when the variables are independent.

3.1  Design goals and visualization principles

• reconnaissance-a preliminary examination, or an overview of a possibly complex terrain;
• exploration-help detect patterns or unusual circumstances, or to suggest hypotheses;
• model building & diagnosis-critique a fitted model as a reasonable statistical summary.

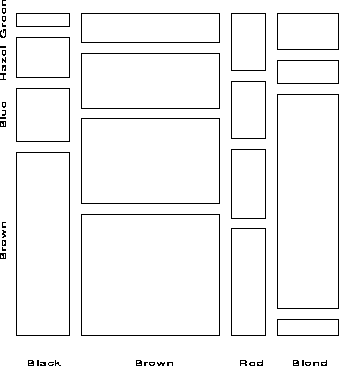
Enhancements to the basic mosaic designed to meet these needs are described below.

3.1.1  Enhanced mosaics

Figure 5 gives the extended the mosaic plot, showing the standardized (Pearson) residual from independence, d_ij = (n_ij - m_ij) / Ö{ m_ij } by the color and shading of each rectangle: cells with positive residuals are outlined with solid lines and filled with slanted lines; negative residuals are outlined with broken lines and filled with grayscale. The absolute value of the residual is portrayed by shading density: cells with absolute values less than 2 are empty; cells with | d_ij | ³ 2 are filled; those with | d_ij | ³ 4 are filled with a darker pattern. Under the assumption of independence, these values roughly correspond to two-tailed probabilities p < .05 and p < .0001 that a given value of | d_ij | exceeds 2 or 4.²

Figure 5: Extended mosaic, reordered and shaded. The two levels of shading density correspond to standardized residuals greater than 2 and 4 in absolute value.

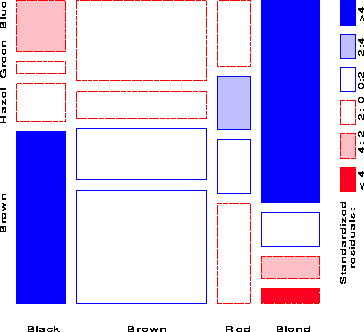
When the row or column variables are unordered, we are also free to rearrange the corresponding categories in the plot to help show the nature of association. For example, in Figure 5, the eye color categories have been permuted so that the residuals from independence have an opposite-corner pattern, with positive values running from bottom-left to top-right corners, negative values along the opposite diagonal. Coupled with size and shading of the tiles, the excess in the black-brown and blond-blue cells, together with the underrepresentation of brown-haired blonds and people with black hair and blue eyes is now quite apparent. Though the table was reordered based on the d_ij values, both dimensions in Figure 5 are ordered from dark to light, suggesting an explanation for the association. In this example the eye-color categories could be reordered by inspection. A general method [ Friendly1994 b] is to sort the categories by their scores on the largest dimension in a (correspondence analysis) singular value decomposition of residuals.

3.1.2  n-way tables

For example, imagine that each cell of the two-way table for hair and eye color is further classified by one or more additional variables-sex and ethnicity, for example. Then each rectangle can be subdivided horizontally to show the proportion of males and females in that cell, and each of those horizontal portions can be subdivided vertically to show the proportions of people of each ethnicity in the hair-eye-sex group.

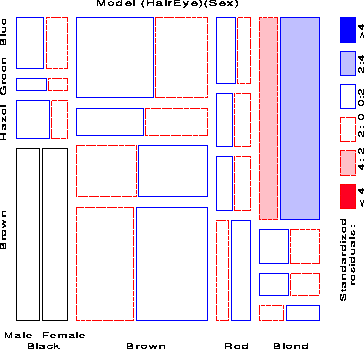
Figure 6 shows the mosaic for the three-way table, with hair and eye color groups divided according to the proportions of Males and Females: We see that there is no systematic association between sex and the combinations of hair and eye color-except among blue-eyed blonds, where there are an overabundance of females. (Do they have more fun?)

Figure 6: Three-way mosaic display for hair color, eye color, and sex. The categories of sex are crossed with those of hair color, but only the first occurrence is labeled. Residuals from the model of joint independence, [HE] [S] are shown by shading. The only lack of fit is an overabundance of females among blue-eyed blonds.

3.2  Fitting models

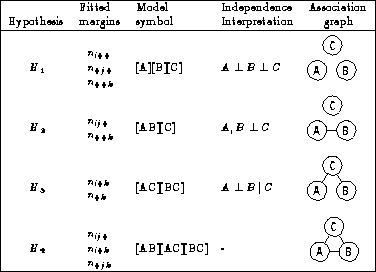
For a three-way table, with variables A, B and C, some of the possible models are described below and summarized in Table 2. I use [ ] notation to list the high-order terms in a hierarchical log-linear model; these correspond to the margins of the table which are fitted exactly. Any other associations present in the data will appear in the pattern of residuals. Here, A ^B is read, ``A is independent of B''. Table 2 also depicts the relations among variables as an association graph, where associated variables are connected by and edge.

H₁: Mutual independence

The model of mutual independence, A ^B ^C, asserts that all joint probabilities p_ijk are products of the one-way marginal probabilities: p_ijk = p_i++  p_+j+  p_++k. This corresponds to the log-linear model [A]  [B]  [C]. Fitting this model leaves all higher terms, and hence all association among the variables, in the residuals.

H₂: Joint independence

The model in which variable C is jointly independent of variables A and B, (A , B ^C ), has p_ijk = p_ij+  p_++k ., and corresponds to the log-linear model [ A B ]  [ C]. Residuals from this model show the extent to which variable C is related to the combinations of variables A and B, but they do not show any association between A and B, since that association is fitted exactly.

H₃: Conditional independence

Two variables, say A and B, are conditionally independent given the third (C) if A and B are independent when we control for C, symbolized as A ^B  |  C. This means that conditional probabilities, p_ij|k, obey p_ij|k = p_i+|k  p_+j|k .. The corresponding log-linear models is denoted [AC]  [BC]. When this model is fit, the mosaic shows the conditional associations between variables A and B, controlling for C, but does not show the associations between A and C, or B and C.

H₄: No three-way interaction

For this model, no pair is marginally or conditionally independent, so there is no independence interpretation. However, the partial association between any two variables is the same at each level of the third variable. The corresponding log-linear model formula is [AB]  [AC]  [BC], indicating that all two-way margins are fit exactly and so are not shown in the residuals. Only a possible three-way association appears in the mosaic.

For example, with the data from Table 1 broken down by sex, fitting the joint-independence model [HairEye][Sex] allows us to see the extent to which the joint distribution of hair-color and eye-color is associated with sex. For this model, the likelihood-ratio G² is 19.86 on 15 df (p = .178), indicating an acceptable overall fit. The three-way mosaic for this model was shown in Figure 6. Any other model fit to this table will have the same tiles in the mosaic since the areas depend on the observed frequencies; the residuals, and hence the shading of the tiles will differ.

3.2.1  Sequential plots and models

The mosaic display is constructed in stages, with the variables listed in a given order. At each stage, the procedure fits a (sub)model to the marginal subtable defined by summing over all variables not yet entered. For example for a three-way table, {ABC}, the marginal subtables {A} and {AB} are calculated in the process of constructing the three-way mosaic. The {A} marginal table can be fit to a model where the categories of variable A are equiprobable (or some other discrete distribution); the independence model can be fit to the {AB} subtable, and so forth. The series of plots can give greater insight into the relationships among all the variables than a single plot alone.

Moreover, the series of mosaic plots fitting submodels of joint independence to the marginal subtables have the special property that they can be viewed as partitioning the hypothesis of mutual independence in the full table [ Friendly1994 b, Goodman1970].

For example, for the hair-eye data, the mosaic displays for the [Hair] [Eye] marginal table (Figure 5) and the [HairEye] [Sex] (Figure 6) table can be viewed as representing the partition

 Model                      df        G2

[Hair] [Eye]                9       146.44
[Hair, Eye] [Sex]          15        19.86
------------------------------------------
[Hair] [Eye] [Sex]         24       155.20

This partitioning scheme for sequential models of joint independence extends directly to higher-way tables. The MOSAICS program [ Friendly1992 b]³ implements a variety of schemes for fitting a sequential series of submodels, including mutual independence, joint independence, conditional independence, partial independence and markov chain models, as shown in Table 3.

3.3  Example: Survival on the Titanic

There have been few marine disasters resulting in the staggering loss of life which occurred in the sinking of the Titanic on April 15, 1912 and (perhaps as a result) few that are so widely known by the public. It is surprising, therefore, that neither the exact death toll from this disaster nor the distributions of death among the passengers and crew are universally agreed. Dawson [ Dawson1995 ] presents the cross-classification of 2201 passengers and crew on the Titanic by Age, Gender, Class (1st, 2nd, 3rd, Crew) shown in Table 4 and describes his efforts to reconcile various historical sources. Let us see what we can learn from this data set.

Examining the series of mosaics for the variables ordered Class, Gender, Age, Survival will show the relationships among the background variables and how these are related to survival. The letters C, G, A, S respectively are used to refer to these variables below.

Figure 7 and Figure 8 show the two-way and three-way plots among the background variables. Figure 7 shows that the proportion of males decreases with increasing economic class, and that the crew was almost entirely male. The three-way plot (Figure 8) shows the distribution of adults and children among the Class-Gender groups. The residuals display the fit of a model in which Age is jointly independent of the the Class-Gender categories. Note that there were no children among the crew, and the overall proportion of children was quite small (about 5 %). Among the passengers, the proportion of children is smallest in first class, largest in third class. The only large positive residuals correspond to a greater number of children among the 3rd class passengers, perhaps representing families travelling or immigrating together.

Figure 7: Titanic data: Class and Gender

Figure 8: Titanic data: Class, Gender, Age

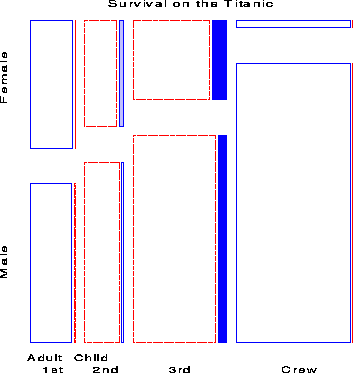
The four-way mosaic, shown in Figure 9, fits the model [CGA][S] which asserts that survival is independent of Class, Gender and Age. This is the minimal null model when the first three variables are explanatory. It is clear that greater proportions of women survived than men in all classes, but with greater proportions of women surviving in the upper two classes. Among males the proportion who survived also increases with economic class. However, this model fits very poorly (G² (15) = 671.96), and we may try to fit a more adequade model by adding associations between survival and the explanatory variables.

Adding a main effect of each of Class, Gender and Age on Survival amounts to fitting the model [CGA][CS][GS][AS]. That is, each of the three variables is associated with survival, but have independent, additive effects. The mosaic for this model, shown in Figure 10. The fit of this model is much improved (DG² (5) = 559.4), but still does not represent an adequate fit (G² (10) = 112.56). There are obviously interactions among Class, Gender and Age on their impact on survival, some of which we have already noted.

Figure 9: Class, Gender, Age, and Survival, Joint independence

Figure 10: Main effects of Age, Gender and Class on Survival

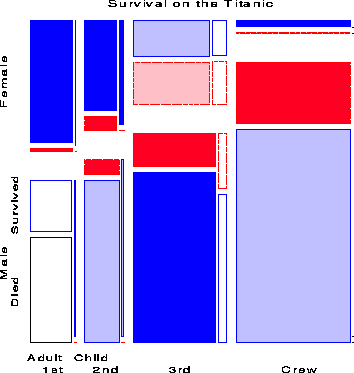
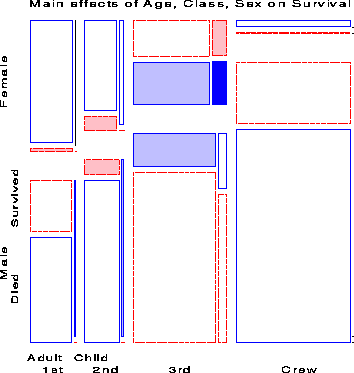
Noting the rubric of ``women and children first'', we next fit the model [CGA][CS][GAS] in which Age and Gender interact in their influence on survival. The mosaic for this model is shown in Figure 11. Adding the association of Age and Gender with survival has improved the model slightly, however the fit is still not good (G² (9) = 94.54). If we add the interaction of Class and Gender to this (the model [CGA][CGS][GAS]) the The likelihood-ratio chi-square is reduced substantially (G² (6) = 37.26), but the lack of fit is still significant.

Finally, we try a model in which Class interacts with both Age and Gender to give the model [CGA][CGS][CAS], whose residuals are shown in Figure 12. The likelihood-ratio chi-square is now 1.69 with 4 df, a very good fit, indeed.

Figure 11: Main effects + Age*Gender on Survival

Figure 12: Main effects + Age*Gender + Class*Gender on Survival

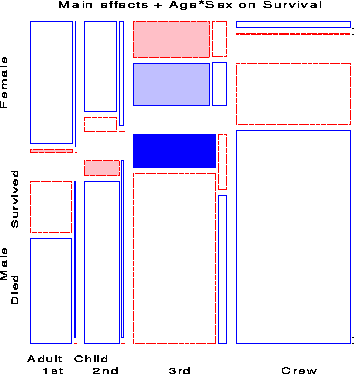
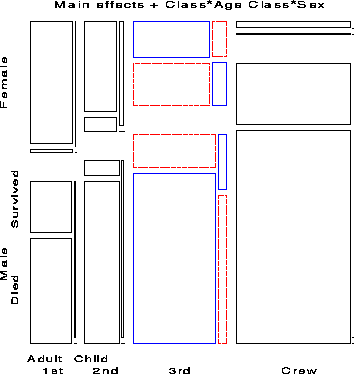
The import of these figures is clear. Regardless of Age and Gender, lower economic status was associated with increased mortality; the differences due to Class were moderated, however, by both Age and Gender. Although women on the Titanic were more likely overall to survive than men, the interaction of Class and Gender shows that women in 3rd class did not have a significant advantage, while men in 1st class did compared to men in other classes. The interaction of Class and Age is explained by the observation that while no children in 1st or 2nd class died, nearly two-thirds in 3rd class died; for adults, mortality increases progressively as economic class declines. Hence, although the phrase ``women and children first'' is melifluous and appeals to our sense of Edwardian chivalry a more adequate description might be ``women and children (according to class), then 1st class men''.

4  Mosaic matrices for categorical data

One reason for the wide usefulness of graphs of quantitative data has been the development of effective, general techniques for dealing with high-dimensional datasets. The scatterplot matrix shows all pairwise (marginal) views of a set of variables in a coherent display, whose design goal is to show the interdependence among the collection of variables as a whole, and which allows detection of patterns which could not readily be discerned from a series of separate graphs. In effect, a multivariate data set in p dimensions (variables) is shown as a collection of p (p-1) two-dimensional scatterplots, each of which is the projection of the cloud of points on two of the variable axes. These ideas can be readily extended to categorical data.

A multiway contingency table of p categorical variables, A, B, C,..., also contains the interdependence among the collection of variables as a whole. The saturated log-linear model, [A B C...] fits this interdependence perfectly, but is often too complex to describe or understand. By summing the table over all variables except two, A and B, say, we obtain a two-variable (marginal) table, showing the bivariate relationship between A and B, which is also a projection of the p-variable relation into the space of two (categorical) variables. If we do this for all p (p-1) unordered pairs of categorical variables and display each two-variable table as a mosaic, we have a categorical analog of the scatterplot matrix, called a mosaic matrix. Like the scatterplot matrix, the mosaic matrix can accommodate any number of variables in principle, but in practice is limited by the resolution of our display to three or four variables.

4.1  MCA and the Burt matrix

Then the Burt matrix is the symmetric partitioned matrix

4.2  Example: Survival on the Titanic

Figure 13 shows the mosaic matrix for the bivariate relations in the Titanic data. The bottom row and the rightmost column show the associations between each of the background variables and Survival collapsing over other variables. There are strong associations of all three variables, but particularly for Gender (females more likely to have survived overall) and for Class (``1st'' most likely to have survived overall). Off-diagonal panels show the associations among the classifications of the passengers and crew. The panel in row 3, column 1⁶ is the bivariate relation between Class and Gender, shown earlier in Figure 7. The panels in row 2 show that very few children sailed on the Titanic, and that most were in 3rd class, and female.

Figure 13: Mosaic matrix of Titanic data. Each panel shows the marginal relation, fitting an independence model between the row and column variable, collapsed over other variable(s).

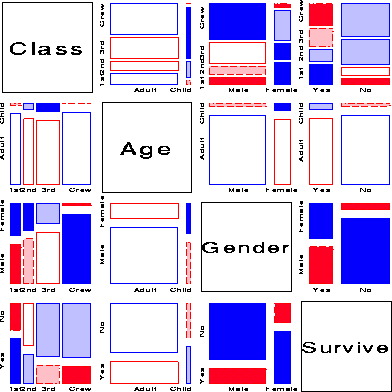
The mosaic matrix in Figure 13 may be compared with the the results of an MCA analysis of the Titanic data. Figure 14 shows the 2-dimensional solution. The positions of the category points for all factors accounts for 50% of the total association (c² (81) = 15533.4), representing all pairwise interactions among the four factors. The points for each factor have the property that the sum of coordinates on each dimension, weighted inversely by the marginal proportions, equals zero, so that high frequency categories (e.g., Adult) are close to the origin. The first dimension is perfectly aligned with the Gender factor, and also strongly aligned with Survival. The second dimension pertains mainly to Class and Age effects. Considering those points which differ from the origin most similarly (in distance and direction) to the point for Survived, gives the interpretation that survival was associated with being female or upper class or (to a lesser degree) being a child.

Figure 14: Titanic data: MCA analysis

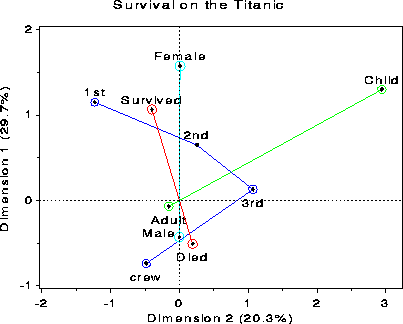
The mosaic matrix, although more complex, captures all of the pairwise associations, while the MCA plot shows only 50% in two dimensions. (A third dimension would account for an additional 17% here.) Most importantly, the pairwise associations are shown explicitly in the mosaic matrix, while they must be inferred from the positions of category points in the MCA plot.

4.3  Example: Berkeley admissions

Figure 15 shows the pairwise marginal relations among the variables Admit, Gender and Department in the Berkeley data which were examined earlier in fourfold displays (Figure 1 and Figure 2). The panel in row 2, column 1 shows that Admission and Gender are strongly associated marginally, as we saw in Figure 1, and overall, males are more often admitted. The diagonally-opposite panel (row 1, column 2) shows the same relation, splitting first by gender.⁷

Figure 15: Mosaic matrix of Berkeley admissions. Each panel shows the marginal relation, fitting an independence model.

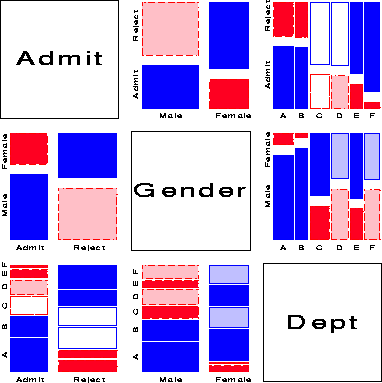
The panels in the third column (and third row) illuminate the explanation for the paradoxical result (see Figure 2) that, within all but department A, the likelihood of admission is equal for men and women, yet, overall, there appears to be a bias in favor of admitting men (see Figure 1) The (1,3) and (3, 1) panels shows the marginal relation between Admission and Department; departments A and B have the greatest overall admission rate, departments E and F the least. The (2, 3) panel shows that men apply in much greater numbers to departments A and B, while women apply in greater numbers to the departments with the lowest overall rate of admission.

4.4  Conditional mosaic matrices

Several further extensions are now possible. First, we need not show the marginal relation between each pair of variables in the mosaic matrix. For example, Figure 16 shows the pairwise conditional relations among these variables, in each case fitting a model of conditional independence with the remaining variable controlled. Thus, the (1,2) and (2,1) panels shows the fit of the model [Admit,Dept] [Gender, Dept], which asserts that Admission and Gender are independent, given (controlling for) department. Except for Department A, this model fits quite well, again indicating lack of gender bias.

Figure 16: Conditional mosaic matrix of Berkeley admissions. Each panel shows the conditional relation, fitting a model of conditional independence model between the row and column variable, controlling for other variable(s)

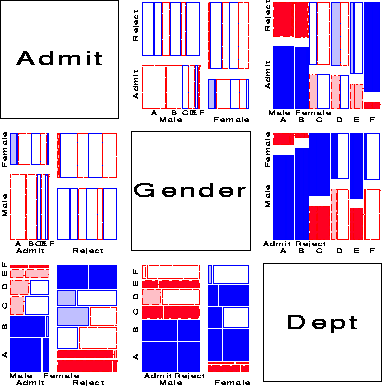
Second, the analogous conditional matrix plot for quantitative variables is of some interest itself. For each pair of variables, X_i, X_j, we plot [(X_i)\tilde] = X_i - [^(X_i)] | others against [(X_j)\tilde] = X_j - [^(X_j)] | others, where ``others'' is the complementary set excluding X_i, X_j. Whittaker shows that X_i, X_j are conditionally independent of the others iff the corresponding element of the inverse covariance matrix S^-1 = { s^ij } is zero,

Third, the framework of the scatterplot matrix can now be used as a general method for displaying marginal or conditional relations among a mixture of quantitative and categorical variables. For marginal plots, pairs of quantitative variables are shown as a scatterplot, while pairs of categorical variables are shown as a mosaic display. Pairs consisting of one quantitative and one categorical variable can be shown as a set of boxplots for each level of the categorical variable. For conditional plots, we fit a model predicting the row variable from the column variable, partialing out (or conditioning on) all other variables from each.

4.5  Coplots for categorical data

One analog of the coplot for categorical data is an array of plots of the dependence among two or more variables, stratified by the values of one or more given variables. Each such panel then shows the partial associations among the foreground variables; the collection of such plots show how these change as the given variables vary. Figure 2 is one example of this idea, using the fourfold display to represent the association in 2 ×2 tables.

For categorical data, models of independence fit to the strata separately have the useful property that they decompose a model of conditional independence fit to the whole table. Consider, for example, the model of conditional independence, A^B |  C for a three-way table. This model asserts that A and B are independent within each level of C. Denote the hypothesis that A and B are independent at level C(k) by A^B |  C(k). Then one can show [ Anderson1991] that

• the overall G² may be decomposed into portions attributable to the AB association in the layers of C, and
• the collection of mosaic displays for the dependence of A and B for each of the levels of C provides a natural visualization of this decomposition.

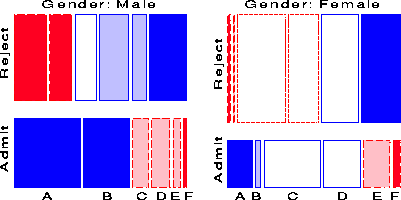
Figure 17 and Figure 18 show two further examples, using the mosaic display to show the partial relations [Admit][Dept] given Gender, and [Admit][Gender] given Dept, respectively. Figure 18 shows the same results displayed in Figure 2: no association between Admission and Gender, except in Dept. A, where females are relatively more likely to gain admission. But one can also see how the proportion admitted decreases regularly from Dept. A to F and how the proportion of females changes across departments. The breakdown of the overall G² from Eqn. (4) is given in Table 5.

Figure 17: Mosaic coplot of Berkeley admissions, given Gender. Each panel shows the partial relation, fitting a model of independence model between Admission and Department.

Figure 18: Mosaic coplot of Berkeley admissions, given Department Each panel shows the partial relation, fitting a model of independence model between Admission and Gender.

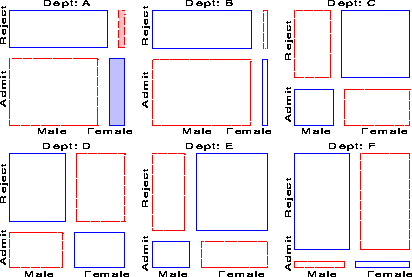
Figure 17 shows that there is a very strong association between Admission and Department-different rates of admission, but also shows two things not seen in other displays: First, the pattern of association is qualitatively similar for both men and women; second the association is quantitatively stronger for men than women-larger differences in admission rates across departments.

4.6 Summary

References

[ Anderson1991]

Anderson, E. B. (1991). Statistical analysis of categorical data. Berlin: Springer-Verlag.

[ Bickel et al.1975]

Bickel, P. J., Hammel, J. W., & O'Connell, J. W. (1975). Sex bias in graduate admissions: Data from Berkeley. Science, 187, 398-403.

[ Cleveland1993]

Cleveland, W. S. (1993). Visualizing data. Summit, NJ: Hobart Press.

[ Dawson1995]

Dawson, R. J. M. (1995). The ``unusual episode'' data revisited. Journal of Statistics Education, 3(3).

[ Fienberg1975]

Fienberg, S. E. (1975). Perspective canada as a social report. Social Indicators Research, 2, 153-174.

[ Friendly1992 a]

Friendly, M. (1992a). Mosaic displays for loglinear models. In ASA, Proceedings of the statistical graphics section  (pp. 61-68). Alexandria, VA.

[ Friendly1992 b]

Friendly, M. (1992b). User's guide for MOSAICS (Tech. Rep. No. 206). York University, Psychology Dept.

[ Friendly1994 a]

Friendly, M. (1994a). A fourfold display for 2 by 2 by k tables (Tech. Rep. No.  217). York University, Psychology Dept.

[ Friendly1994 b]

Friendly, M. (1994b). Mosaic displays for multi-way contingency tables. Journal of the American Statistical Association, 89, 190-200.

[ Friendly1994 c]

Friendly, M. (1994c). SAS/IML graphics for fourfold displays. Observations, 3(4), 47-56.

[ Friendly1995]

Friendly, M. (1995). Conceptual and visual models for categorical data. Amer. Statistician, 49, 153-160.

[ Friendly1997]

Friendly, M. (1997). Conceptual models for visualizing contingency table data. In M. Greenacre & J. Blasius (Eds.), Visualization of categorical data (pp. 17-35). San Diego, CA: Academic Press.

[ Friendly1998]

Friendly, M. (1998). Visualizing categorical data. In M. Sirken, D. Herrmann, S. Schechter, N. Schwarz, J. Tanur, & R. Tourangeau (Eds.), Cognition and survey research (pp.  ??-??). New York: Wiley. (In press)

[ Goodman1970]

Goodman, L. A. (1970). The multivariate analysis of qualitative data: Interactions among multiple classifications. Journal of the American Statistical Association, 226-256. (65)

[ Greenacre1984]

Greenacre, M. (1984). Theory and applications of correspondence analysis. London: Academic Press.

[ Hartigan & Kleiner1981]

Hartigan, J. A., & Kleiner, B. (1981). Mosaics for contingency tables. In W. F. Eddy (Ed.), Computer science and statistics: Proceedings of the 13th symposium on the interface (pp. 286-273). New York: Springer-Verlag.

[ Hartigan & Kleiner1984]

Hartigan, J. A., & Kleiner, B. (1984). A mosaic of television ratings. Amer. Statistician, 38, 32-35.

[ Snee1974]

Snee, R. D. (1974). Graphical display of two-way contingency tables. Amer. Statistician, 28, 9-12.

[ Tukey1993]

Tukey, J. W. (1993). Graphic comparisons of several linked aspects: Alternative and suggested principles. Journal of Computational and Statistical Graphics, 2(1), 1-33.

[ Whittaker1990]

Whittaker, J. (1990). Graphical models in applied multivariate statistics. Wiley.

drew.tex, processed Jul 17, 1998

Footnotes:

¹ This explanation ignores the possibility of structural bias against women, e.g., lack of resources allocated to departments that attract women applicants.

² For exploratory purposes, we do not usually make adjustments (e.g., Bonferroni) for multiple tests because the goal is to display the pattern of residuals in the table as a whole. However, the number and values of these cutoffs can be easily set by the user.

³ http://www.math.yorku.ca/SCS/mosaics.html

⁴ In all cases, the model [A]  [B] is fit to a two-way table or marginal table.

⁵ The representation would be complete if the one-way margins where drawn in the diagonal cells.

⁶ Rows and columns in the mosaic matrix are identified as in a table or numerical matrix, with row 1, column 1 in the upper left corner.

⁷ Note that this is different than just the transpose or interchange of horizontal and vertical dimensions as in the scatterplot matrix, because the mosaic display splits the total frequency first by the horizontal variable and then (conditionally) by the vertical variable. The areas of all corresponding tiles are the same in each diagonally opposite pair, however, as are the residuals shown by color and shading.