Matrix Algebra Problems with Applications in Psychology and Multivariate Analysis

Multivariate Data Analysis
Michael Friendly
York University

Psychology 6140

Students in Multivariate Analysis need to develop skills in working with matrices and reading matrix expressions. Some of the skills which seem to be important are:

1. Performing simple matrix calculations
2. Manipulating algebraic expressions in matrices-substituting identities, simplifying expressions, etc.
3. Formulating substantive and statistical problems in matrix terms-or, recognizing such in journal articles.
4. Understanding certain key results (theorems) of matrix algebra.
5. Recognizing these results when they are used in your text.

The following problems are directed toward developing these skills. Along the way, some matrix applications in psychology and multivariate statistics are introduced.

I.  Elementary matrix expressions

1. Factoring a matrix into the product of two matrices is the basis of many methods in multivariate analysis. Choleski's method involves factoring a matrix into the product of two triangular matrices, one of which has 0s above the diagonal, the other below the diagonal. Fill in the ?

   Hint: Let each ? be an unknown letter; solve the equations.

   entries in the following matrix equations:

   1. 
      

      é ê ë 5 10 2 7 ù ú û     =     é ê ë ? 0 ? ? ù ú û     ×    é ê ë 1 ? 0 1 ù ú û

   2. 
      

      é ê ê ê ë 3 -3 6 -1 5 14 -3 1 12 ù ú ú ú û     =     é ê ê ê ë ? 0 0 ? ? 0 ? ? ? ù ú ú ú û     ×    é ê ê ê ë 1 ? ? 0 1 ? 0 0 1 ù ú ú ú û

2. Premultiply the matrix M by each of the following matrices. Describe in words in each case what effect the premultiplier has on the rows of M.

   
   

   M = é ê ê ê ë a1 b1 c1 a2 b2 c2 a3 b3 c3 ù ú ú ú û

   
   

   A = é ê ê ê ë 0 1 0 1 0 0 0 0 1 ù ú ú ú û    B = é ê ê ê ë 0 0 1 0 1 0 1 0 0 ù ú ú ú û    C = é ê ê ê ë 1 2 0 0 1 0 0 0 1 ù ú ú ú û

3. Let D be an m ×n matrix and let e_i  =  ( 0, 0, ¼, 1, 0, ¼, 0 )¢ denote the n-dimensional vector consisting of zeros except for the i-th element, which is 1.

   1. What is D  e_i (in words)?
   2. Express the matrices A and B from Problem 12 above in terms of e vectors.
4. Experimenters in color vision have found that a subject can match any spot of colored light by an additive mixture of three colored lights of fixed spectral composition (Judd, 1951). Any three colors can be used as the primary lights provided that none is a combination of the other two.

   Say that an experimenter has a colorimeter that has three primary lights with values r, g, and b. She wants to specify her results in terms of a standard set of tri-stimulus values, R, G, and B. By experiment she finds that the amount of each of the standard primaries needed to match each of his primaries is

   
   

   r = a11  R + a12  G + a13  B g = a21  R + a22  G + a23  B b = a31  R + a32  G + a33  B

   Define the appropriate vectors and matrices to express the above system of equations in matrix terms.

5. Let x = (x₁,¼,x_n)¢ be a vector containing the number of units purchased of each of a variety of grocery items. Let y = (y₁,¼,y_n)¢ be a vector of unit prices, such that y_i = the price/unit of item i. For example, x = ( 4 ,  3 ,  2 ) ¢ and y = (.95 ,  .25 ,  6.50 ) ¢ might represent 4 dozen eggs at $0.95 per dozen, 3 lbs. of apples at $0.25/lb, and 2 cans of pate de fois gras at $6.50 per can (cheap, if it's entier).

   1. Formulate a matrix expresstion for the total (net) cost of the commodities in x.
   2. Suppose each commoditiy is subject to a particular rate of tax, these being given by a vector, t = t₁,¼,t_n¢ so that if commodity i is taxed at 5%, t_i = 0.05. Formulate an expression in terms of matrices and vectors for the total cost of x including taxes. [Remember, cost after tax = net cost × ( 1 + t).]
6. Cliff (1959) showed that the affective value of an adverb-adjective combination (e.g., moderately nice) could be predicted quite accurately by multiplying an affective value for the adjective (nice) by an intensity value for the adverb (moderately).

   Suppose one took a set of m personality-trait adjectives like industrious, happy, carefree, shy, etc. and formed all possible combinations of these with n adverbs, seldom, somewhat, moderately, extremely-m ×n pairs.

   If a group of people rated each combination on an evaluative scale, the average ratings could be assembled in an m ×n matrix, C = { c_ij } = average rating of adverb i and adjective j. Let v = (v₁,¼,v_m )¢ be a vector of intensity values for the adverbs and d = (d₁,¼,d_n)¢ be a vector of average ratings for the adjectives by themselves. Cliff's model was:

   
   

   cij = vi ×dj + k

   where k is a constant. [Cliff's model fit the data rather well, in fact, and created considerable interest in the possibility of developing mathematical models of aspects of language.]

   1. Express C in this model as a product of two matrices.

      Hint: The number of summed terms is the number of columns in a matrix product.

   2. If this model holds, what is the rank of C?

7. A quadratic function of a scalar variable, x can be written

   
   

   f ( x ) = b0 + b1  x + b2  x2

   1. Express f ( x ) as an algebraic expression of the vectors b = ( b₀ ,  b₁ ,  b₂ ) ¢ and x = ( 1 ,  x ,  x² ) ¢.
   2. In terms of this expression, evaluate f ( 2 ) for b = ( b₀ ,  b₁ ,  b₂ ) ¢.
   3. Generalize to find an expression for an n-th degree polynomial of x,

      
      

      f ( x ) = b0 + b1  x + b2  x2+ ¼+ bn  xn

   4. If person i has a value of x_i, let x_i be the vector ( 1 ,  x_i ,  x_i² ) ¢. Write a matrix expression which will give the values of f ( x_i ) as a vector for all persons in a group.
   [Completing this question, you have just (re-)discovered the General Linear Model!]
8. Let j_n be a column vector of n unities (ones). Using the following vectors,

   
   

   a = ( 1, 3, 5 ) ¢       c = ( 2, 1, 1 ) ¢ b = ( -5, 2, 3 ) ¢       x = ( x1 , x2 , x3 )¢

   find each of the following inner products with j₃. State in words the effect of taking an inner product with j_n.

   1. a¢ j₃
   2. b¢ j₃
   3. j¢₃  c
   4. x¢ j₃
   [Matrix notation was invented to simplify the expression of linear equations. The operation of multiplying vectors by the unit vector has a particularly simple interpretation.]
9. Let X be a N ×p matrix consisting of the scores of N people on p tests, where x_ij = the score of person i on test j. Define the matrix Z   ( N ×p ) of standard scores, z_ij = ( x_ij  -  [`x]_j )  /  s_j. From the fact that the correlation between two standardized variables is r_ij = ( [1/N] ) å_{i = 1}^N z_ji  z_ik, show that the p ×p matrix of all intercorrelations can be expressed as

   
   

   R = ( 1 N ) Z ¢ Z

   [In standard scores, the correlation is simply the average cross-product. Isn't that nice?]

II.  Applications: Choice, preference and graph theory

The problems in this section deal with applications of matrix algebra to representing relationships among objects by matrices and directed or undirected graphs. Two basic type of relations between objects can be represented in this way: An incidence matrix contains entries of 0 or 1 in cell i, j to indicate that the object in row i is related in a symmetric way to the object in column j. A dominance or preference matrix also uses binary entries, but the relation is not necessarily symmetric, as in ``person i likes person j'', or ``player i beats player j'' in a tournament.

1. In a sociometric experiment, members of a group are asked which other members they like. Suppose the data are collected in a choice diagram as given in Figure 1, where an arrow going from i to j means that ``i likes j''.
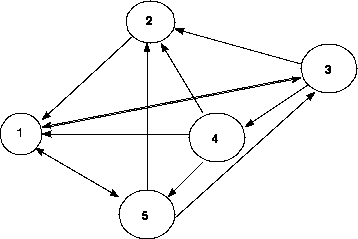   Figure 1: Directed graph for a sociometric experiment. A directed arrow points from a person to the person he/she likes.

   1. Convert the diagram to a matrix, C, where c_ij = 1 if i likes j, and 0 otherwise. The diagonal elements, c_ii = 0.
   2. Let u be an n ×1 vector with unit elements. One might say that u ¢ C gives scores for ``popularity''. Explain why.
   3. Explain how C  u can be interpreted as scores for ``generosity''.
2. Suppose B is a similar matrix of choices, where

   
   

   bij = ì í î 1 i likes j -1 i dislikes j

   Imagine a similar matrix, P , where p_ij = 1 if j believes that i likes him and p_ij = - 1 if j believes that i dislikes him. The diagonal elements of B and P are equal to 0.

   1. Let N = P ¢ B, so that n_ij = åp_ki  b_kj. Explain why n_ij can be interpreted as a measure of ``identification'' between person i and person j.
   2. Determine whether the diagonal elements of N can be interpreted as a measure of ``realism'' (k is realistic if his beliefs about who likes him agree with reality).
   3. Determine whether the diagonal elements of B   P¢ can be interpreted as a measure of ``overtness'' (k is overt if his beliefs about X conform to X's likes and dislikes).
   4. Compute the matrix C² = C ×C and interpret the elements of this matrix.
   5. Try also to find an interpretation for the elements of C³.
   6. Is there any interpretation you can come up with for the elements of C  C ¢ or C ¢ C?
3. The expression, u ¢ C, where u is a unit vector, tells how often a person is liked, so it is a measure of popularity. Suppose two persons are chosen equally often, but the first is liked by popular people and the second is liked by less popular people; then it may be reasonable to say that the first person is more popular, since he/she has more indirect choices.

   Suppose now we want to combine direct and indirect choices in a measure of popularity, defined as follows: Define a ``transmission'' parameter, 0 < p < 1, and assume that each direct choice contributes an amount p to a person's popularity; an indirect choice through one intermediate person contributes an amount p²; an indirect choice through two intermediates contributes an amount p³, etc.

   1. Show that the measure that takes into account all indirect choices in this way can be found from the vector u ¢T, where

      
      

      T = p  C +p2  C2 +p3  C3 + ¼+p n-1  C n-1

      (1)

   2. Show that the following identity holds for T defined above:

      
      

      T  ( I - p  C ) = p  C

      (2)

      This equation provides a way to solve for T without evaluating the entire matrix sum in equation (1).

      Hint: Form a second equation by multiplying (1) by C, and subtract.

   3. Show that equation (2) above is equivalent to

      
      

      t ¢ ( I - p  C ) = p   s

      where, t ¢ = u¢T and s ¢ = u¢C. [Source: Van de Geer (1971)]

4. Consider a hypothetical sociometric choice matrix for three people, as in the previous problem:

   
   

   C = é ê ê ê ë 0 1 0 1 0 1 1 0 0 ù ú ú ú û

   and assume that the quantity p, the relative effectiveness of transmission thru a sociometric link, has the value 1/2. Solve for the respective elements of t, the vector of status indices.

5. In a paired comparison experiment, a subject is presented with all pairs of stimuli that can be formed out of a set (e.g., political candidates), and is asked to indicate for each pair which stimulus he prefers. For n stimuli, the data can be collected in square matrix, X of order n  ×  n where x_ij = 1 if j is preferred to i and is 0 otherwise. The diagonal elements are zero.

   1. Verify that if x_ij   =  1 then x_ji   =   0 where i ¹ j.
   2. Figure 2 gives a diagram of choices, where an arrow going from i to j indicates that i is preferred to j. Convert this diagram to a choice matrix X.
      Figure 2: Choice graph for a paired comparison experiment.

   3. Calculate u¢ X where u is a unit vector and interpret the elements of the resulting vector.
   4. Rearrange the rows and columns of X in such a way that all 1 elements are above the diagonal, so the result is a triangular matrix. Interpret the order of the rows and columns in this new matrix.
   5. Inspection of the diagram reveals that all choices are transitive, that is for any three stimuli, if i is preferred to j and j to k, then i is always preferred to k. If k were preferred to i, we would have a circular triad. Draw a diagram in which circular triads do occur, and convert it to the corresponding choice matrix. Calculate u ¢ X for this matrix, and compare the value for the result for a transitive matrix.
   6. Let v = u ¢ X. Compare the values of v ¢ v as calculated from the figure with those calculated from the matrix X you constructed in part (e). What effect does the presence of circular triads have on the values of v = u ¢ X?
6. The problem in archeology of placing sites and artifacts in proper chronological order is called sequence dating or seriation. The same problem, of ``putting in order'' arises in developmental psychology and test theory, but the context in archeology is simplest.

   An assumption made in archeology is that graves which are ``close together'' in temporal order will be more likely to have similar contents than graves further apart in time. Consider the situation in which various types of pottery, P₁ ,  P₂ ,  ... P_n are contained in graves G₁ ,  G₂ ,  ... G_m. Let A be the m ×n matrix with elements,

   
   

   aij = ì í î 1 if Gi   contains Pj 0 if Gi   doesn¢t contain Pj

   1. Show that the element g_ij of the matrix G = A  A ¢ is equal to the number of common varieties of pottery found in both graves G_i and G_j.
   2. Show that the diagonal element, g_ii of G gives the number of varieties of pottery in grave G_i
   3. Show that the archeological assumption stated above is equivalent to the statement that the larger the g_ij, the closer the graves G_i and G_j are in time.
   4. If five types of pottery are contained in four graves according to the matrix A below, find G, and arrange the four graves in time order.

      
      

      A = é ê ê ê ê ë 1 1 0 1 1 0 0 1 0 1 0 1 1 0 1 1 1 1 1 1 ù ú ú ú ú û

   [Source: Williams (198?), Kendall (1969)]
7. In a Markov model for short term serial recall, Murdock (1976) suggests that an item (e.g., nonsense syllables, like DAXUR) may be in any one of three states for a learner:

   state IO

   where both item and order information have been retained (i.e., the learner remembers the elements of the item and the order in which they occurred).

   state I

   where only item information is retained (i.e., s/he remembers it contained D, A, X, U, R but not what order they were in).

   state N

   where neither type of information is retained.

   A Markov model is specified by identifying the states and by specifying a ``transition matrix'', which contains the probabilities that the item changes from one state to another. In Murdock's model, the transition probabilities are shown symbolically in the matrix T below.

   
   

   T = é ê ê ê ë 1-a a(1-b) ab 0 1-c c 0 0 1 ù ú ú ú û

   The parameters are defined as follows:

   • a gives the probability that an item will leave the state IO.
   • If it leaves that state, b is the probability that item information as well as order information will be forgotten.
   • Given that the item is in state I (order information has not been retained), c is the probability that item information will be forgotten as well.

   A characteristic of the Markov model is that these probabilities apply to each interval of time, Dt during the retention interval. Murdock further assumes that at the start of the retention interval, an item starts in state IO with probability p, and with probability 1 - p it starts in state I. The psychological rational here might be that encoding an item at all establishes item information, and something more is required for the learner to encode serial order too. An attentive subject would never miss an item completely (Murdock assumes), so there is no probability that an item starts in state N. These starting state probabilities can be put in a vector, s,

   
   

   s = ( p ,  1 - p ,  0 )

   1. Show that the probabilities that an item is in any of the states, IO, I, or N after 1 time interval, D  t is s ¢ T.
   2. Show that after 2 transition intervals, the probabilities are s ¢ T ×T = s ¢ T², and after 2 time intervals, they are s¢ T³. [You may reason from the result of part (a), together with the diagram above, rather than multiplying the symbolic matrix entries.]
   3. Assume parameter values of p = 1.0, a = b = 0.1, and c = 0.5. Find the probabilities that an item is in state IO, I, and N after 1, 2, and 3 transitions.
8. The matrix M below represents the performance of five people on three binary items, where m_ij = 1 indicates that item i is answered correctly by person j.

   
   

   M = é ê ê ê ë 1 1 1 0 0 0 1 0 1 1 1 0 1 0 1 ù ú ú ú û

   1. Calculate the product M M¢. What do the diagonal elements represent? What do the off-diagonal elements represent?
   2. Calculate the product M¢ M. What do the diagonal elements represent? What do the off-diagonal elements represent?
9. In studies of perceptual identification, it is common to present stimuli (say, letters) in a background of noise and require the subject to identify the stimulus seen or heard. For n stimuli, the results are collected in an n ×n matrix, X, where

   
   

   xij = Prob ( subject says  j  |   stimulus i was presented )

   In studying the relationships between stimuli in such a matrix, it is sometimes assumed that confusions are symmetric, x_ij = x_ji, but for some types of stimuli, the results are not symmetric.

   1. Express the average proportion of correct responses as a function of the elements of X.
   2. Show that an arbitrary square matrix, X can be expressed as the sum of two matrices,

      
      

      X = S + A

      where S = ( X + X ¢) / 2 is symmetric, and A is a skew-symmetric matrix, i.e., a_ij = - a_ji.

   3. Why might it be reasonable to regard A as containing ``pure asymmetry'' information and S as containing ``pure symmetry'' information?
   [Psychological models for perceptual identification sometimes assume symmetry for errors, and sometimes do not. The decomposition of X allows both to be studied.]

III.  Bases, orthogonality and vector spaces

1. On a sheet of graph paper,

   1. Draw directed lines from the origin to represent the vectors,

      
      

      a ¢ = ( 1 ,  0 )       p ¢ = ( 4 ,  1 ) b ¢ = ( 0 ,  1 )       q ¢ = ( 2 ,  3 )

   2. Draw on the graph directed lines which represent the vectors:

      
      

      r = p - q s = q - p t = p + q/ 2

   3. The vectors a and b form a basis for the two-dimensional vector space of the graph paper. Show that each of p, q, r, s, and t can be expressed as linear combinations of a, and b of the form,

      
      

      n  a + m  b

      where n and m are real numbers.

   4. The vectors p and q also form a basis for this vector space. Show that a, and b can be expressed as linear combinations of p, and q of the form, u  p + v  q where u and v are real numbers.
2. Show that the vector c = ( c₁ ,  c₂ ,  ...  c_n ) ¢ is orthogonal to the vector
   ( 1 , 1 ,  ¼  1 )  ¸Ön if and only if å _{i = 1} ⁿ  c_i = 0.
3. Consider the set of (n - 1) n-dimensional vectors:

   
   

   c1 ¢ = ( 1, -1, 0, 0, ..., 0 ) ¸Ö2 c2 ¢ = ( 1, 1, -2, 0, ..., 0 ) ¸Ö6 c3 ¢ = ( 1, 1, 1, -3, 0, ..., 0 ) ¸Ö12 ¼ c n-1 ¢ = ( 1, 1, 1, 1, ..., 1, -(n-1) ) ¸   ______ Ö n2 - n

   These vectors are referred to as Helmert contrasts . They are useful for comparing ANOVA factors whose levels are ordered, but not quantitative. Show that for n = 5 the vectors, c₁  , c₂  , ..., c _{n - 1} :

   1. are all orthonormal (i.e., pairwise orthogonal and of unit length).
   2. are all orthogonal to the unit vector, j_n.
   3. any other vector d, which is orthogonal to the unit vector, j_n. can be expressed as a linear combination of c₁, c₂, ..., c _{n - 1} .
   These three facts imply together that any other set of contrasts among n levels can be expressed in terms of c₁, c₂, ..., c _{n - 1} . Isn't that nice?
4. Consider the n ×n matrix

   
   

   C = é ê ê ê ê ë 1-n 1 1 ¼ 1 1 1-n 1 ¼ 1 ¼ ¼ ¼ ¼ ¼ 1 1 1 ¼ 1-n ù ú ú ú ú û

   1. Show that rank( C ) = n - 1.
   2. Show that C  j = 0. That is, j is orthogonal to every row of C, so C is the orthogonal complement of j.
   3. Let x_· = ( x _·1 ,  x _·2 ,  ...,  x _{· n} ) ¢ be the means of n treatment groups in a single factor experiment. Interpret x_·¢ j .
   4. Evaluate C  x_·. Using the results of (a), (b), and (c) above, show that C  x_· is a vector of n contrasts among the group means, of which only n - 1 are independent. What do these contrasts represent?
5. If c₁ , c₂ , ...,  c_n are vectors, all orthogonal to a vector x, show that any vector in the span of c₁ , c₂ , ..., c_n is orthogonal to x.
6. Show that any linear combination of a set of independent contrasts is also a contrast.
7. Given the three 4-dimensional vectors below, suppose we wish to find a unit-length vector, x, which is orthogonal to each.

   
   

   c1 = ( -1, -1, 0, 0 ) ¢ c2 = ( 0, 2, -1, -1 ) ¢ c3 = ( 3, -2, 0, -1 ) ¢

   1. Show that x must satisfy c₁ ¢  x   =  c₂ ¢ x   =  c₃ ¢ x   =  0.
   2. What additional equation must x satisfy?
   3. Find x.
8. Find two unit vectors, a, and b, which are each orthogonal to the vector, m = 1 ¸Ö3  ( 1,  1,  1 ) ¢.
9. The general linear model, written in matrix notation, is given by

   
   

   y = X b + e

   (3)

   where y is an n ×1 observation vector, X is an n ×p design matrix, b is an p ×1 vector of unknown parameters, and e is an n ×1 random vector of residuals. For regression models, X is typically a unit column vector followed by columns of predictor variables. For ANOVA models, X is typically a unit vector followed by columns of indicator (0/1) variables.

   1. Consider a two-way 2 ×3 ANOVA design with n = 1 observation per cell (Elswick etal, 1991). If the model (without interaction) is given by

      
      

      yij = m+ ai + bj + eij,    i = 1:2; j = 1:3

      (4)

      and the vector of parameters is b¢ = ( m, a₁, a₂, b₁, b₂, b₃ ) , find the design matrix X so that the elements in y (a 6 by 1 vector) can be expressed in the form of Eqn. (3).

   2. By considering linear dependencies among the columns of X, determine the rank of X. Hazard a guess about the relation between rank and degrees of freedom.
   3. Find the row echelon form X^* of X (Try the ECHELON function in APL or SAS
      IML). Does this confirm your observation of the rank of X?
   4. The product X^* b shows the linear combinations of the elements of b which can be estimated from the data. Find X^* b and interpret the result.

IV.  Transformations, projections & quadratic forms

1. Let x = ( x₁ ,  x₂ ) ¢ be a 2-dimensional vector and consider a rotation in which the vector is rotated counter-clockwise about the origin through an angle of q degrees, to a position, x^* = ( x₁^* ,   x₂^* ), as shown in Figure 3. In scalar terms, the rotation can be expressed as

   
   

   x1* = x1  cosq- x2  sinq x2* = x1  sinq+ x2  cosq

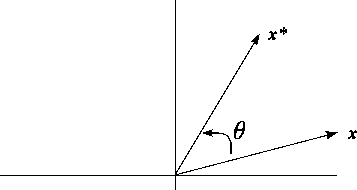   Figure 3: Rotation of a vector in 2-dimensional space

   1. Find the matrix T in the matrix expression of the above equations, x^* = T  x.
   2. Show that this matrix T is orthonormal.
2. Let L be a matrix of factor loadings of a set of tests with respect to one set of coordinate axes. If the coordinates are rotated, the matrix equation for expressing the matrix V of loadings with respect to the rotated axes is V = L  T. Suppose there are four tests and two factors, and L is given by

   
   

   L = é ê ê ê ê ë .52 .30 .35 .20 .40 .69 .30 .52 ù ú ú ú ú û

   1. Find a matrix T representing a transformation through a positive angle of 30^°.
   2. Evaluate the product, L  T, rounding to two decimals. Note that some elements in V = L  T. are (approximately) zero. The principle of simple structure in factor rotation seeks a rotation for which many elements of the rotated matrix become zero.
3. The rotation procedure of factor analysis can be expressed as a set of linear transformations, i.e., as a matrix product. Let V = L  T represent such a linear transformation. The matrix L is a factor matrix satisfying R = L  L¢, where R is the correlation matrix V is the transformed factor matrix, and T is a matrix of coefficients which specifies the rotation.

   1. Find a condition on the matrix T such that the transformed factor matrix, V will also satisfy the factor equation.
   2. Show that the particular matrix T of problem 1 satisfies this condition, within rounding error.
4. Consider a simple two-dimensional example in which three tests have these loadings on two underlying factors:

            Factor1  Factor2
   Test 1     0.50    0.30
   Test 2     0.30    0.20
   Test 3    -0.40    0.70
   
   

   Each test can be represented as a point in the plane of Factor1 (x-axis) and Factor2 (y-axis). Plot these test points, and find their transformed coordinates when the coordinate axes are rotated through a positive angle of 37^°. Use sin37^° = 0.60,  cos 37^° = 0.80.

5. Let x   =  ( x₁ ,  x₂ ) ¢, and

   
   

   A = é ê ë 2 2 4 -2 ù ú û  ,     B = é ê ë 1/2 0 0 1 ù ú û

   Expand the following quadratic forms:

   1. x ¢ A  x
   2. x ¢ B  x
   3. Describe in words the difference between the expansions in (a) and (b).
6. Describe (or plot) the set of points with coordinates ( x, y ) that satisfy the matrix equations:

   Hint: Multiply out, then repeat: {substitute a trial value for x and solve for y}

   .

   1. 
      

      æ è x y ö ø   é ê ë 4 0 0 5 ù ú û   æ ç è x y ö ÷ ø = 60

   2. 
      

      (x , y)   é ê ë 4 3 3 5 ù ú û   æ ç è x y ö ÷ ø = 60

7. Evaluate the quadratic forms, u ¢ A  u , where u   =  ( x,  y,  1 ) ¢ and where the matrix A is:

   
   

   (a) é ê ê ê ë 0 0 -2a 0 1 0 -2a 0 0 ù ú ú ú û    (b) é ê ê ê ë 1 0 0 0 1 0 0 0 4 ù ú ú ú û    (c) é ê ê ê ë a 0 b 0 0 -1 b -1 c ù ú ú ú û    (d) é ê ê ê ë 0 1 0 1 0 0 0 0 -4 ù ú ú ú û

   What functions would be obtained by setting each of these quadratic forms equal to 0?

8. The next few problems demonstrate how some of the common expressions for sums of squares can be represented by quadratic forms. Suppose n observations are represented by a vector x = ( x₁ ,  x₂ ,  ..., x_n ) and the sample variance is based on the sum of squared deviations,

   
   

   SS = n å i = 1    ( xi  -  _ x   )2 = n å i = 1    xi2 - n _ x   2

   Show that

   1. [`x] = ( 1 / n )  x ¢ j.
   2. Sx_i² = x ¢ x.
   3. n   [`x]² = ( 1 / n )  x ¢ J  x = ( 1 / n )  x ¢j   j ¢ x, where J is the n   × n matrix with all elements equal to 1.
   4. Hence, show that SS can be expressed by the quadratic form,

      
      

      SS = x ¢ ( I - J / n )  x

   5. Write out explicitly the matrix ( I - J / n ) for n = 3. [Source: Searle, 1966]
9. ANOVA and regression tests are based on breaking up sums of squares into independent, additive portions attributable to various sources of variance. This problem demonstrates some of the properties of the quadratic forms associated with these sums of squares.

   Consider the well-known identity for a set of test scores, y_i ,  i = 1,  ...,  n:

   
   

   n å i   yi2 = n _ y   2   + n å i  ( yi  -  _ y   )2

   (5)

   In the previous problem, it was shown that the sum of squared deviations term could be written as a quadratic form,

   
   

   y ¢ ( I - J / n )  y = y ¢ A2  y        (say)

   1. Show that the above identity (3) can be written as

      
      

      y ¢ A0  y = y ¢ A1  y + y ¢ A2  y

      where A₀ ,  A₁ ,  A₂ are n ×n symmetric. Find A₀ and A₁ .

   2. Show that the following properties hold:

      
      

      A0 = A1 + A2 A1 = A1 2 A2 = A2 2 A1  A2 = 0

   3. Show that:

      
      

      tr ( A0 ) = n     = rank( A0 ) tr ( A1 ) = 1     = rank( A1 ) tr ( A2 ) = n-1    = rank( A2 )

      Matrices such as A₁ and A₂ with these properties are called idempotent projection matrices. Every sum of squares formula such as (3) in ANOVA and regression can be represented as a sum of quadratic forms with idempotent projection matrices.

   4. Evaluate the expression,

      
      

      y ¢ A1  y  /  1 y ¢ A2  y  /   n  - 1

      for y = ( 2 , 3 , 3 , 3 , 5 , 8 )¢. Interpret this expression and state what statistical test it is used in.

10. In psychological experiments, response classes are often defined arbitrarily. As a result, an experimenter may wish to combine response classes when he analyzes data. In formal models it is useful to have a representation of this procedure of combining response classes.

    Bush, Mosteller & Thompson (1954) use a projection matrix to combine responses. An example is the matrix,

    
    

    P = é ê ê ê ë 1 0 0 0 1 1 0 0 0 ù ú ú ú û

    This matrix is used as follows: Let there be three response classes initially, with probabilities, r₁ ,  r₂ ,   and r₃, in a column vector, r.

    1. Postmultiply P by r, and describe verbally the result.
    2. Show that the matrix P satisfies P² = P.
11. Guttman (1944) discusses a method of factoring a correlation matrix, based on the equation,

    
    

    f = R x ( x ¢R x )- 1/2

    (6)

    where f is one column of a factor matrix, F; R is the correlation matrix; and x is a column vector containing arbitrarily selected coefficients. Once a single factor has been found using this method, the same formula can be applied to the residual correlation matrix, R₁ = R - f  f  ¢, to find a second factor, and so forth. A factor matrix F which is build up in this way will always satisfy the basic equation of factor analysis, F  F ¢ = R.

    Suppose that the matrix of intercorrelations on four tests is

    
    

    R = é ê ê ê ê ë .64 .56 .48 .40 .56 .49 .42 .35 .48 .42 .36 .30 .40 .35 .30 .25 ù ú ú ú ú û

    The elements on the main diagonal of R are not 1.0 as would be ordinarily expected, but are values called communalities. representing the variance of each test which is shared with the other tests.

    1. Apply Guttman's formula (4) to the matrix R to find a single column f of the factor matrix. Assume x to be the vector x = (1,  1, 1, 1 ) ¢
    2. Show that in this case, f  f ¢ = R, or equivalently, R₁ = R - f f ¢ = 0. In other words, the only one factor can account for all the correlations in R.
    [Congradualtions! You've just discovered the basis for factor analysis.]
12. Resolve the column vector x = ( x₁ ,  x₂ ,   x₃ ) ¢ into two components, x_a and x_b , such that

    1. x = x_a + x_b
    2. x_a is parallel to the vector ( 1 ,  1 ,   1 )  / Ö3
    3. x_b is perpendicular (orthogonal) to ( 1 ,  1 ,  1 )  / Ö3
    [And now, the Gram-Schmidt method for transforming correlated variables into orthongonal ones!]
13. Arbuckle and Friendly (1977) consider the problem of transforming a vector of factor loadings, x to a vector y so that y is as smooth as possible in the sense that the sum of squares of successive differences, å_{i = 1}^{n - 1} ( y_i  - y_{i + 1} )² is as small as possible.

    1. Find an (n-1) ×n matrix P such that

       
       

       P  y = é ê ê ê ê ë y1 - y2 y2 - y3 : yn-1 - yn ù ú ú ú ú û = d   (say)

    2. Show that the sum of squares of successive differences referred to above is given by d ¢ d .
    3. If y is obtained as a linear combination of x, by y = T  x, find an expression not using parentheses to express the sum of squared successive differences in terms of T, x, and P.

V.  Determinants, inverse, and rank

1. Find the inverse of

   
   

   A = é ê ë 5 3 3 2 ù ú û

2. 1. Verify that the inverse of

      
      

      é ê ë 3 0 0 1/5 ù ú û     is     é ê ë 1/3 0 0 5 ù ú û

   2. What is the inverse of

      
      

      é ê ë a 0 0 b ù ú û

      Can you determine what the inverse of any diagonal matrix is?

3. If

   
   

   A = é ê ë a11 a12 a21 a22 ù ú û

   show that | A | = a₁₁ a₂₂ - a₂₁ a₁₂ = a₁₁ ( a₂₂ - a₂₁ a₁₁^-1 a₁₂ ). This last expression has an important analog for partitioned matrices.

4. A frequent question in the testing field is whether to add another test to a battery of n tests to attempt to increase the prediction of an external criterion. Horst (1951) proposes a time-saving method of answering this question. He derives a formula for the validity of an additional test, k, that would be required to increase the validity of the battery by an amount a.

   Let R be the (n+1) ×(n+1) matrix of intercorrelations, partitioned with test k as the last row and column,

   
   

   R = é ê ë R* rk rk ¢ 1 ù ú û

   where R^* is the n ×n matrix of correlations of all tests except test k, and r_k is the column vector of correlations of test k with each other test.

   To develop his formula, Horst needed to find the inverse of R, that is a matrix S, such that R  S = I, the identity matrix. Thus, S = R^-1.

   1. Partition the matrix S conformably with R, as

      
      

      S = é ê ë S* u u ¢ d ù ú û

      and write out the equation R  S = I in terms of partitioned matrices.

   2. Write out the four sub-matrix equations implied by the equation in part (a).
   3. Find S = R^-1 by solving for S^*, u, and d.
5. If a matrix is upper (lower) triangular, then its inverse is also upper (lower) triangular. Show that this is true for the matrix S below by finding its inverse.

   
   

   S = é ê ê ê ë 1 2 -1 0 1 3 0 0 1 ù ú ú ú û

   Hint: Let

   
   

   S-1 = é ê ê ê ë a b c d e f g h i ù ú ú ú û

   and write out the 9 scalar equations implied by S^-1  S = I.

6. In a ratio scaling experiment four stimuli are presented in all possible pairs to the subject. For each pair, the subject is required to give a number representing the relative ``strength'' of the first stimulus compared to the second. For example, he/she may be asked to judge the relative brightness of two lights, or which of two tones is higher in pitch.

   One hypothesis for this type of judgment is that the subject has internal subjective intensity values for each stimulus, and to make a judgment, ``computes'' and reports the ratio of the two values for a pair.

   Let the matrix R = { r_ij } contain the judgments of each pair, for stimulus i relative to stimulus j, and let s = ( s₁ , ...,  s_n ) ¢ be a vector of the subject's internal scale values for these stimuli.

   1. Express the hypothesis, r_ij = s_i ¸s_j in matrix terms.
   2. What does this hypothesis imply about the rank of R if the model holds?
   3. What does this imply about the latent roots of R ¢  R?
7. In the randomized block design, each of n subjects is given each of a series of p experimental treatments, resulting in a score, y_ij = score of subject i under treatment j. With one observation per cell, the standard analysis of variance model (without interaction) is,

   
   

   yij = ai + bj     ( + eij )

   1. Write Y (n ×p) = y_ij and express Y in terms of a_i, and b_j as a product of two matrices.
   2. Tukey's ``one degree of freedom for non-additivity'' adds an additional term to this model, giving:

      
      

      yij = ai + bj + g  ai bj     ( + eij  )

      where g is one additional parameter to be estimated. Write a matrix product expression for Y in this model. [You may not simply multiply Y by the identity matrix. Use no + signs in the elements in the factors in your product.]

   3. What is the rank of Y if the model of part (a) holds?
   4. What is the rank of Y if the model of part (b) holds?
8. Suppose an animal running a maze is scored under 3 experimental conditions for (a) number of wrong turns made, (b) number of pauses, and (c) time to reach the goal. Some data is given below, with scores expressed as deviations from the column means.

             Errors  Pauses  Time
   Cond. 1     2       0       4
   Cond. 2     1       6      10
   Cond. 3    -3      -6     -14
   
   

   1. Determine the rank of this matrix.
   2. If time and errors have been measured, does the pause measure contribute any additional information?
   3. If e is the (column vector) number of errors, p is the number of pauses, and t the time taken, can you find a constant a to make the following equation true for these data?

      
      

      t = a  e + 4 3  p

VI.  Simultaneous equations

1. On a sheet of graph paper draw lines representing each of the three linear equations,

   
   

   x - y = 0 (1) 3x - 2y = 1 (2) 4x - 2y = 3 (3)

   1. Show that this system of equations has no solution and interpret this fact with reference to your geometrical interpretation.
   2. Suppose we adopt the following procedure for ``solving'' the system. Take the equations and solve them in pairs- (1) and (2), (1) and (3), (2) and (3). This will give values, say ( x<sub>1</sub> ,  y<sub>1</sub> ), ( x<sub>2</sub> ,  y<sub>2</sub> ), and ( x<sub>3</sub> ,  y<sub>3</sub> ) which may not agree. ``Solve'' the equations in this way and locate the solution points on your graph.
   3. Now, suppose we adopt as the final solution to this system the average value,

      
      

      ( _ x   , _ y   ) = æ ç è (x1 + x2 + x3 ) 3 , (y1 + y2 + y3 ) 3 ö ÷ ø

      Locate this point on your graph and interpret geometrically.

2. Show that the system of equations,

   
   

   x = 1 - y 2x + 2y = 2

   is underdetermined. That is, there is no unique pair ( x , y ) which satisfy both equations.

   1. Draw these two equations as lines on a graph and explain why there is no unique solution.
   2. If the second equation is changed to 2 x + 2 y = 3, explain why these two equations become inconsistent.

VII.  Latent roots and vectors

Multiplication of a vector v by a square matrix A can be regarded as a mapping or transformation of v into some other vector, v^* in the vector space,

A  v = v*

A latent vector, or eigenvector of the matrix A is a special vector whose direction is unchanged by that transformation. That is, if v is a non-zero vector such that

A  v = k  v

then v is an eigenvector or latent vector of A, and k, the constant of proportionality, is the eigenvalue or latent root corresponding to v.

1. In Householder's method for determining eigenvalues of a real symmetric matrix, A, the matrix is subjected to a series of orthogonal transformations of the form

   
   

   P = I - 2  w  w ¢        where w ¢ w = 1

   1. Show that P is orthonormal and symmetric.
   2. If the latent roots of A are l₁ ,  l₂ , ..., l_n, what are the latent roots of P  A  P ?
   3. If the latent vectors of A are v₁ ,  v₂ , ..., v_n, what are the latent vectors of P  A  P ?
2. The eigenvalues and eigenvectors of any square, symmetric matrix A  ( n ×n ) can (in principle) be found by (1) finding the n values of l which satisfy | A - lI |   =  0; (2) solving A v = lv for v using each value of l determined by step (1). Using this method, find the eigenvalues and eigenvectors of the following matrices:

   
   

   (a) é ê ë 1 1 0 1 ù ú û             (b) é ê ë 0 -1 1 -1 ù ú û

3. Show that the eigenvalues of the matrix

   
   

   é ê ë cosq sinq sinq -cosq ù ú û

   are ±1.

4. In the Markov model for serial learning outlined in Problem 27 verify that the eigenvalues of the transition matrix, T are

   Hint: Solve the characteristic equation | T - lI | = 0.

   
   

   l = ì ï í ï î 1 1-c 1-a

5. A magic square is a matrix in which the elements of each row, column and the two main diagonals add up to the same number, this number being called the magic number For the magic square, A, below, show that one latent root of this magic square is its magic number. (This is true for all magic squares).

   
   

   A = æ ç ç ç è 8 1 6 3 5 7 4 9 2 ö ÷ ÷ ÷ ø

References

[1]

Arbuckle, J. & Friendly, M.L. (1977). On rotating to smooth functions. Psychometrika, 42, 127-140.

[2]

Bush, R.R., Mosteller, F. & Thompson, G.L. (1954). A formal structure for multiple choice situations. In Thrall, Coombs & Davis (Eds.) Decision processes. NY: Wiley.

[3]

Cliff, N. (1959). Adverbs multiply adjectives. Psychological Review, 66, 27-44.

[]

Elswick, R. K., Jr., Gennings, C., Chinchilli, V. M., and Dawson, K. S. (1991). A simple approach for finding estimable functions in linear models. The American Statistician, 45, 51-53.

[4]

Guttman, L. (1944). General theory and methods of matric factoring. Psychometrika, 9, 1-16.

[5]

Horst, P. (1951). The relation between the validity of a single test and its contribution to the predictive efficiency of a test battery. Psychometrika, 16, 57-66.

[6]

Judd, D.B. (1951). Basic correlates of the visual stimulus. In S. S. Stevens (Ed.) Handbook of experimental psychology New York: Wiley.

[7]

Kendall, D. G. (1969). Some problems and methods in statistical archaeology. World Archaeology, 1, 61-.

[8]

Kendall, M.G. (1962). Rank correlation methods London: Griffin.

[9]

Murdock, B. B. Jr. (1976). Item and order information in short-term serial memory. Journal of Experimental Psychology: General, 105, 191-216.

[10]

Searle, S.R. (1966). Matrix algebra for the social sciences New York: Wiley.

[11]

Van de Geer, J.P. (1971). Introduction to multivariate analysis for the social sciences San Francisco: W. H. Freeman.

[12]

Williams, G. (198?). Mathematics in archaeology. Mathematics Teacher, ?, 56-58.