[Previous] [Next] [Up] [Top] Categorical Data Analysis with Graphics
Michael Friendly

Part 1: Plots for discrete distributions

Discrete frequency distributions often involve counts of occurrences such as accidental fatalities, words in passages of text, or blood cells with some characteristic. Typically such data consist of a table which records that n sub k of the observations pertain to the basic outcome value k , k = 0 , 1, ... .

The table below shows two such data sets:

von Bortkiewicz's (1898) data on death of soldiers in the Prussian army from kicks by horses and mules. The data pertain to 10 army corps, each observed over 20 years. In 109 corps-years, no deaths occurred; 65 corps-years had one death, etc. ( Figure 1)
Mosteller & Wallace's (1964) data on the occurrence of the word may in 262 blocks of text (each about 200 words long) from issues of the Federalist Papers known to be written by James Madison. In 156 blocks, the word may did not occur; it occurred once in 63 blocks, etc. ( Figure 2)

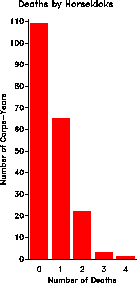
    Deaths by Horsekick          Occurrences of 'may'

        k    nk                    k    nk
       ----------                 ----------
        0    109                   0    156
        1     65                   1     63
        2     22                   2     29
        3      3                   3      8
        4      1                   4      4
           -----                   5      1
           N=200                   6      1
                                      -----
                                      N=256

Figure 1: von Bortkiewicz's data Figure 2: Mosteller & Wallace data

Fitting a probability distribution

Often interest is focussed on how closely such data follow a particular distribution, such as the Poisson, binomial, or geometric distribution. Usually this is examined with a classical goodness-of-fit chi-square test,

chi² = Sum from k=1 to K < ( n sub k - N p hat sub k ) > sup 2 over < N p hat sub k > ~ chi² ( K-1 )

where p hat sub k is the estimated probability of each basic count, under the hypothesis that the data follows the chosen distribution.

For example, for the Poisson distribution, the probability function is

(1)

The maximum likelihood estimator of the parameter lambda is just the mean of the distribution,

lambda Hat = Sigma k n sub k / N

For the horsekick data, the mean is 122/200 = .610, and calculation of Poisson probabilities (PHAT), expected frequencies, and contributions to chi² are shown below.

 k     nk      p        phat         exp     chisq

 0    109    0.545    0.54335    108.670    0.00100
 1     65    0.325    0.33144     66.289    0.02506
 2     22    0.110    0.10109     20.218    0.15705
 3      3    0.015    0.02056      4.111    0.30025
 4      1    0.005    0.00313      0.627    0.22201
      ===                        =======    =======
      200                        199.915    0.70537 ~  chi² (4)

In this case the chi² shows an exceptionally good (unreasonably good?) fit. In the word frequency example, the fit of the Poisson turns out not to be close at all. However, even a close fit may show something interesting, if we know how to look; conversely, it is useful to know why or where the data differ from a chosen model.

(von Bortkiewicz's data is collapsed over 20 years and 14 army corps, and the Poisson model assumes that the probability of a death is constant for all years and corps. This assumption can be tested in the raw data, by fitting a poisson model, deaths = year corps. The effects of both year and corps are significant, indicating that the homogeneity assumption is not met.)

Poissonness plot

The poissonness plot (Hoaglin, 1980) is designed as a plot of some quantity against k , so that the result will be points along a straight line when the data follow a Poisson distribution. When the data deviate from a Poisson, the points will be curved. Hoaglin & Tukey (1985) develop similar plots for other discrete distributions, including the binomial, negative binomial, and logarithmic series distributions.

Assume, for some fixed lambda , each observed frequency, n sub k equals the expected frequency, m sub k = N p sub k . Then, setting n sub k = N p sub k = { e sup {- lambda} lambda sup k } / { k ! } , and taking logs of both sides gives

log ( n sub k ) = log N - lambda + k log lambda - log k !

which can be rearranged to

(2)

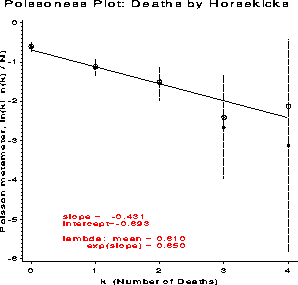
The left side of (2) is called the count metameter , and denoted phi ( n sub k ) = < k ! n sub k > / N . Hence, plotting phi ( n sub k ) against k should give a line with

intercept = - lambda
slope = log lambda

Features of the poissonness plot

Resistance : a single discrepant value of n sub k affects only the point at value k .
Comparison standard : An approximate confidence interval can be found for each point, indicating its inherent variability and helping to judge whether each point is discrepant.
Influence : Extensions of the method result in plots which show the effect of each point on the estimate of the main parameter of the distribution ( lambda in the Poisson).

The calculations for the poissonness plot, including confidence intervals, is shown below for the horse kicks data. See the plot in Figure 3.

         phi (n sub k)
                         CI       CI      Confidence Int
k    nk        Y       center   width     lower    upper

0   109   -0.607      -0.617    0.130    -0.748   -0.487
1    65   -1.124      -1.138    0.207    -1.345   -0.931
2    22   -1.514      -1.549    0.417    -1.966   -1.132
3     3   -2.408      -2.666    1.318    -3.984   -1.348
4     1   -2.120      -3.120    2.689    -5.809   -0.432

Figure 3: Poissonness plots for two discrete distributions. The Horse Kicks data fits the Poisson distribution reasonably well, but the May data does not.

Drawbacks

A different formula for the count metameter, phi ( n sub k ) is required for each discrete distribution.
Systematic deviation from a linear relationship does not indicate which distribution provides a better fit.

Ord plots

An alternative plot suggested by Ord (1967) may be used to diagnose the form of the discrete distribution. Ord showed that a linear relationship of the form,

(3)

holds for each of the Poisson, binomial, negative binomial, and logarithmic series distributions. The slope, b , is zero for the Poisson, negative for the binomial, and positive for the negative binomial and logarithmic series distributions, which are distinguished by their theoretical intercepts.

Thus, a plot of k n sub k / n sub k-1 against k , if linear, is suggested as a means to determine which distribution to apply.

+--------------------+--------------------------------------+
|   Slope  Intercept |     Distribution         Parameter   |
|    (b)     (a)     |     (parameter)          estimate    |
|--------------------+--------------------------------------|
|     0       +      |   Poisson (lambda)      lambda = a   |
|                    |                                      |
|     -       +      |   Binomial (n, p)       p = b/(b-1)  |
|                    |                                      |
|     +       +      |   Neg. binom (n,p)      p = 1 - b    |
|                    |                                      |
|     +       -      |   Log. series (theta)   theta =  b   |
|                    |                         theta = - a  |
+--------------------+--------------------------------------+

Fitting the line

In the small number of cases I've tried, I have found that using a weighted least squares fit of k n sub k / n sub k-1 on k , using weights of w sub k = sqrt < n sub k -1 > produces reasonably good automatic diagnosis of the form of a probability distribution.

Examples

The table below shows the calculations for the horse kicks data, with the ratio < k p sub k > / < p sub k-1 > labeled y. The weighted least squares line, with weights w sub k , has a slope close to zero, indicating the Poisson distribution. The estimate lambda = a = .656 compares favorably with the value from the Poissonness plot.

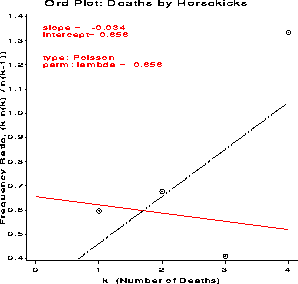
           Ord Plot: Deaths by Horsekicks

       k     nk    nk)       wk         y

       0    109      .    10.3923     .         -- Weighted LS --
       1     65    109     8.0000    0.5963     slope = -0.034
       2     22     65     4.5826    0.6769     inter = 0.656
       3      3     22     1.4142    0.4091
       4      1      3     0.0000    1.3333

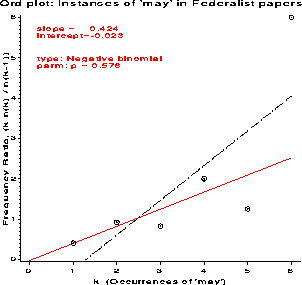
For the word frequency data, the slope is positive, so either the negative binomial or log series are possible. The intercept is essentially zero, which is ambiguous. However, the logarithmic series requires b approx - a , so the negative binomial is a better choice. Mosteller & Wallace did in fact find a reasonably good fit to this distribution.

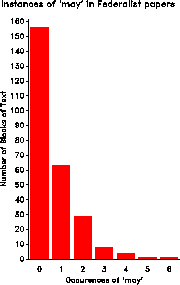
           Instances of 'may' in Federalist papers

       k     nk    nk)       wk         y

       0    156      .    12.4499     .       -- Weighted LS --
       1     63    156     7.8740    0.4038   slope = 0.424
       2     29     63     5.2915    0.9206   inter = -0.023
       3      8     29     2.6458    0.8276
       4      4      8     1.7321    2.0000
       5      1      4     0.0000    1.2500
       6      1      1     0.0000    6.0000

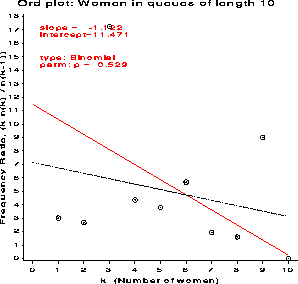
Plots of data fitting several different discrete distributions are shown in Figure 4.

Drawbacks

The Ord plot lacks resistance, since a single discrepant frequency affects the points for k and k + 1 .
The sampling variance of k n sub k / n sub k-1 fluctuates widely. The use of weights w sub k helps, but is purely a heuristic device.

Figure 4: Ord plots for four discrete distributions. The OLS line is drawn in black, the WLS line in red. The slope and intercept of the WLS line are used to automatically diagnose the type of the distribution.

[Previous] [Next] [Up] [Top]

Contents