boxcox Power transformations by Box-Cox method boxcox

SAS Macro Programs: boxcox

$Version: 1.4 (21 Aug 2002)
Michael Friendly
York University

The boxcox macro ( [download] get boxcox.sas)

Power transformations by Box-Cox method

The boxcox macro finds maximum likelihood power (or folded power) transformations of the response variable in a regression model by the Box-Cox method. The program provides graphic displays of the maximum likelihood solution, t-values for model effects, and the influence of observations on choice of power. The program can produce printer plots or high-resolution versions of any of these plots. The optimal transformation of the response variable is returned in an output dataset.

For a positive response variable, y > 0, the family of monotone power transformations with power p is
y(p) = (yp - 1) / p p != 0
log (y) p = 0
If the response contains 0 or negative values, use the ADD= parameter to assure that y+&ADD is strictly positive.

If the response variable is bounded on a closed interval, [0, b], the FOLD= parameter may be used to obtain analogous folded-power transformations. For example, use FOLD=100 when the response variable is a percentage on the interval [0, 100].

Method

The program uses transforms the response to all powers from the LOPOWER= value to the HIPOWER= value, and fits a regression model for each, extracting values to an output dataset from which the plots are drawn.

The influence plot also implements a score test for the power transformation due to Atkinson, which provides an alternative estimate of the power transformation, based on power = 1 - slope of the fitted line in the partial regression plot for a constructed variable.

Usage

boxcox is a macro program. A value must be supplied for the RESP= parameter.

The arguments may be listed within parentheses in any order, separated by commas. For example: 

   %boxcox(resp=responsevariable, model=predictors, ..., )

Parameters

RESP=
The name of the response variable for analysis.
MODEL=
A blank-separated list of the independent variables in the regression, i.e., the terms on the right side of the = sign in the MODEL statement for PROC REG. The MODEL= terms may be empty to obtain a transformation of a response on its own.
DATA=_LAST_
The name of the data set holding the response and predictor variables. (Default: most recently created)
ID=
The name of an ID variable for observations, used in labeling the influence plot. (Default: ID=_N_)
FOLD=0
Upper bound for the response variable. If FOLD>0 is specified, folded power transformations are computed. E.g., for a response which is a proprotion, specify FOLD=1; for a percentage, specify FOLD=100.
OUT=_DATA_
The name of an output dataset to contain the transformed response. This dataset contains all original variables, with the transformed response replacing the original variable.
OUTPLOT=_PLOT_
The name of the output data set containing _RMSE_, and t-values for each effect in the model, with one observation for each power value tried.
PPLOT=RMSE EFFECT INFL
Which printer plots should be produced? One or more of RMSE, EFFECT, and INFL, or NONE.
GPLOT=RMSE EFFECT INFL
Which high-resolution (PROC GPLOT) plots should be produced? One or more of RMSE, EFFECT, and INFL, or NONE.
LOPOWER=-2
low value for power
HIPOWER=2
high value for power
NPOWER=21
number of power values in the interval LOPOWER to HIPOWER
CONF=.95
confidence coefficient for the confidence interval for the power.

Example

The example finds power transformations for the MPG variable in the auto dataset, using Weight, Displacement and Gear Ratio as predictors. 
%include data(auto);
%include macros(boxcox);     * or, store in autocall library;
%boxcox(data=auto,
         resp=MPG,
         model=Weight Displa Gratio,
         id=model,
         gplot=RMSE EFFECT INFL,
         lopower=-2.5, hipower=2.5, conf=.99);
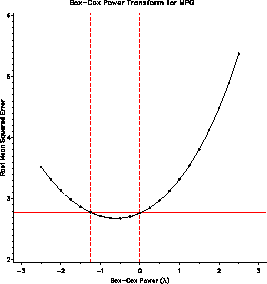
The plot of RMSE vs. lambda (power) indicates power = -1 / sqrt(MPG) as the maximum likelihood estimate, but power = -1 / MPG == gallons/mile is within the confidence interval.

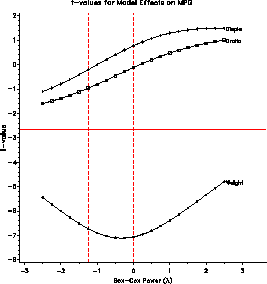
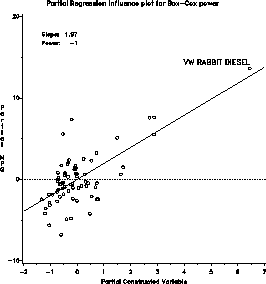
The EFFECT plot indicates that the significance of partial t-test are unaffected by the choice of power. The influence plot indicates that the VW Diesel has a large leverage, but is not influential in determining the choice of power.

See also

boxglm Power transformations by Box-Cox method for GLM
boxtid Power transformations by Box-Tidwell method
nqplot Normal QQ plot
outlier Robust multivariate outlier detection
resline Resistant line for bivariate data
stars Diagnostic plots for transformations to symmetry