Among the most important problems of the 17th century were those concerned with physical measurement-
of time, distance, and space- for astronomy, surveying, map making, navigation and territorial expansion.
This century saw great new growth in theory and the dawn of practice- the rise of analytic
geometry, theories of errors of measurement
and estimation, the birth of probability theory
, and the beginnings of demographic statistics
and
``political arithmetic''.
By the end of this century, the necessary elements were at hand-
some real data of significant interest, some theory to make sense of them,
and a few ideas for their visual representation. Perhaps more importantly,
one can see this century as giving rise to the beginnings of visual thinking.
- early 1600s
-
Tables of empirical data, published tables of numbers begin to appear. ``Die Tabellen-Statistik,'' as a branch of
statistics devoted to the numerical description of facts- Germany.
- 1603
-
Tables, and first world map showing lines of geomagnetism (isogons), used in work on finding longitude by means of magnetic
variation. The tables give the world distribution of the variation,
by latitude, along each of the meridians- Guillaume Le Nautonier (1557-1620), France
[209,181].

PIC: Le Nautonier portrait (156 x 199; 56K)
TXT: Biographical sketch
FIG: Le Nautonier's geomagentic map (566 x 381; 93K)
FIG: Modern re-creation of the magnetic equator after Le Nautonier (888 x 459; 16K)
- 1603
-
The pantograph was invented for mechanically copying a figure on an enlarged or reduced scale- Christopher Scheiner (1575-1650), Italy.

PIC: Scheiner's portrait
FIG: Scheiner's pantograph (224 x 136; 4.5K)
TXT: Scheiner's sunspots, equatorial mount and pantograph
- 1610
-
The first astronomical pictures ever printed, from observations through a telescope,
used to illustrate discoveries of craters on the moon, the 4 staelites of Jupiter and a vast
number of stars never seen by unaided eyes- Galileo Galilei (1564-1642), Italy
[95]

FIG: Cover page from Sidereus Nuncius (500 x 672; 81K)
FIG: Page 9v: craters on the moon (226 x 366; 32K)
TXT: Works of Galileo: Starry Messenger
- 1614
-
Invention of logarithms, and the first published tables of logarithms- John Napier (1550-1617), Scotland [208].

PIC: Napier portrait (268 x 326; 9.6K)
FIG: Two pages from Napier's table of logarithms (1330 x 1014; 352K)
FIG: Diagram of spherical triangles from [208] (500 x 760; 42K)
TXT: Biography of Napier
TXT: Text of A Description of the Admirable Table of Logarithms (with images)
- 1617
-
First use of Frisius' method of trigonometric triangulation to produce locations of major cities in Holland; foundation of geodesy-
Willebrord van Roijen Snell (Snellius) (1580-1626), Leiden, Netherlands [269].
PIC: Snellius portrait (200 x 257; 49K)
TXT: Snell, biographical sketch
In 1621, Willibrord Snell, in \emph{Cyclometricus}, discovered the law of refraction which says that the ratio of the sines of the angles of incidence and refraction is a constant and the index of refraction varies from one transparent substance to another. This law implies that the velocity of light in a medium is inversely proportional to its refractive index. Cyclometricus was published after Snell's death by Rene' Descartes.
- 1620-1628
-
Invention of a mechanical device, containing a logarithmic scale of equal parts and trigonomic functions which, with the aid of a pair of calipers, could be used
as a slide rule. This device, called ``Gunter's scale,'' or the ``gunter'' by seamen, was soon replaced by a true slide rule, containing two parallel logarithmic
scales- Edmund Gunter (1581-1626) and William Oughtred (1574-1660), England [10,115].

TXT: Edmund Gunter - Biographical sketch
TXT: Edmund Gunter - Biography
TXT: William Oughtred - Biography
IMG: Gunter's log scale(398 x 39; 0.5K)
IMG: Oughtred's dual log scale (442 x 52; 1K)
FIG: Gunter's scale image (2200 x 176; 110K)
- 1623
-
The first known adding machine, a mechanical calculator
called the ``Calculating Clock.'' It could add and subtract up to six-digit numbers,
based on the movement of six dented wheels geared through a ``mutilated''
wheel which with every full turn allowed the wheel located at the right
to rotate 1/10th of a full turn-Wilhelm Schickard (1592-1635), Tubingen, Germany.

FIG: reproduction of Schickard's calculating clock (300 x 244; 34K)
TXT: Schickard biography
TXT: History of mechanical calculators - Part 1
- 1626
-
Visual representations used to chart the changes in sunspots over time. Also, the first known use of the idea of ``small multiples''
to show a series of images in a coherent display- Christopher Scheiner (1575-1650), Italy [259].
IMG: Scheiner sunspot image (135 x 150; 4K)
FIG: Apparatus for recording sunspots (600 x 320; 68K)
TXT: A brief history of sunspots
FIG: Sunspot plate from Scheiner's ``Tres Epistolae'' (650 x 505; 250K)
- 1632
-
Statistical analysis of observations on location of Tycho Brahe's star of 1572, based on idea that the most probable hypothesis is the one having the smallest (least absolute value) deviations- Galileo Galilei (1564-1642), Italy [96] [116,§ 10.3].
PIC: Galileo portrait (190 x 187; 4K)
TXT: Galileo biography
- 1637
-
Coordinate system reintroduced in mathematics, analytic geometry; relationship established between graphed line and equation-Pierre de Fermat (1601-1665) and René Descartes (1596-1650), France [59].
PIC: Descartes portrait (200 x 248; 18K)
TXT: Biographical sketch - Rene Descartes
TXT: Biographical sketch - Pierre de Fermat
About 1629, Pierre de Fermat discovered that the equation $f(x,y)=0$ represents a curve in the xy-plane. This is the fundamental principle of analytic geometry, and was first published by Descartes in 1637. He also formulated a method for determining the maximim and minimum values which give single solutions for problems which in general have two solutions. This procedure is ``almost precisely that now given in the differential calculus''`` ''(Boyer 1949:156).
- 1644
-
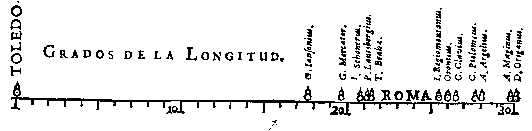
First visual representation of statistical data: variations in determination of longitude between Toledo and Rome- Michael
F. van Langren (1598-1675), Spain [171].
IMG: Langren image (532 x 131; 11K)
- 1646
-
Invention of the first projection lantern (the magic lantern).
[Images were painted on glass and
projected on walls. Kirscher, a Jesuit priest, was the last recorded ordained priest openly to concern
himself with optics. Henceforth, the art of
projecting images was classified as an entertainment and curtailed.]- Athanasius Kirscher (1602-1680), Germany [160].

PIC: Althanasius Kircher portrait (180 x 220; 39K)
IMG: a Sturm Lantern, 1676 (100 x 120; 1K)
TXT: Jesuits and the Sciences, 1660-1719
TXT: Jesuits and the Sciences, 1660-1719
- 1654
-
Initial statements of the theory of probability- Blaise Pascal (1623-1662) and Pierre de Fermat (1601-1665), France.
PIC: Pascal portrait (200 x 229; 41K)
TXT: Pascal biography, extract from [13]
- 1654
-
The first large scale attempt at a scientific, economic survey (of the Irish estates confiscated by Oliver Cromwell), perhaps the first econometric study,
leading to development of political arithmetic-
William Petty (1623-1687), Ireland [230,233]
 .
.
PIC: William Petty portrait (200 x 240; 37K)
FIG: Map of William Petty's Down Survey (350 x 305; 26K)
TXT: Petty - Biographical profile, with links to works and resources
TXT: Political Arithmetick, by Sir William Petty
- 1657
-
First text on probability- Christiaan Huygens (1629-1695), Netherlands [145].
PIC: Huygens portrait (216 x 192; 9K)
TXT: Biographical blurb from [13]
TXT: English translation of De Ratiociniis in Ludo Aleae
- 1663
-
Automatic recording device (the weather clock) producing a moving graph of temperature and wind direction (in polar coordinates)- Christopher Wren (1632-1723), England [22,327].
PIC: Wren portrait (210 x 290; 10K)
PIC: Wren portrait (268 x 326; 16K)
TXT: Wren catalog entry from the Galileo Project
TXT: Wren biography (St. Andrews)
- 1662
-
Founding of demographic statistics: Development of the idea that vital statistics (records of christenings and burials in London) could be used to construct life tables.
The average life expectancy in London was 27 years, with 65% dying by age 16- John Graunt (1620-1674), England, [110,275].
PIC: Graunt portrait (526 x 762; 75K)
IMG: Title page of Graunt's Bills of Mortality (309 x 387; 5K)
FIG: Mortality table, from [230] (1000 x 795; 237K)
TXT: Text of Graunt's ``Observations on the Bills of
Mortailty''
Graunt's work of 1662 is often ascribed to Sir William Petty. The authorship question
has been discussed by Wilcox \cite{Wilcox:1937}, who concludes that although a portion of
the work was by Petty, the majority is due to Graunt.
- 1666
-
First modern complete demographic census, a record of each individual by name of the 3215 inhabitants of New France-
Jean Talon (1626-1694), Canada [108,p. 179],[154,p. xix].
TXT: Commentary on first Canadian census by Dan
TXT: The great intendant: A chronicle of Jean Talon in Canada (e-book)
TXT: Jean Talon biography from Statistics Canada
E. H. Godfrey says that this is ``a date prior to any modern census, whether European or American'', see \cite[p. 179]{Godfrey:1918}. The returns were fairly complete, giving data on population, sexes, families, conjugal condition, age, profession and trades, and they filled 154 pages. The original copy is now in the Archives of Paris, and a transcript in the Archives of Ottawa.
- 1669
-
First graph of a continuous distribution function, a graph of Gaunt's life table, and a demonstration of how to find the median remaining lifetime for a person of given age- Christiaan Huygens (1629-1695), Netherlands [32]
IMG: see [116,Fig. 8.1.1].
IMG: Huygens graph (301 x 284; 1K)
TXT: Huygens - Biographical sketch
TXT: Complete works of Huygens
Source: correspondence between Huygens and his brother Lodewijk.
- 1671
-
First attempt to determine scientifically what should be the purchase price of annuities, using mortality tables- Jan de Witt (1625-1672), Netherlands [326].

PIC: de Witt portrait (82 x 109; 5K)
TXT: de Witt biography
TXT: Death and Statistics, including an account of de Witt's method
- 1686
-
Bivariate plot of a theoretical curve derived from observations (barometric pressure vs. altitude), graphical analysis based on empirical data- Edmond Halley (1656-1742), England [118].
PIC: Halley portrait (254 x 326; 21K)
FIG: Halley's graph of change in barometric pressure (914 x 773; 7K)
- 1686
-
First known weather map, showing prevailing winds on a geographical map of the Earth- Edmond Halley (1656-1742), England
[117].
PIC: Halley portrait (254 x 326; 21K)
FIG: Halley's wind map, 1686 (512 x 196; 24K)
FIG: Halley's wind map, section 1 detail (739 x 627; 122K)
TXT: Halley - Biographical sketch
- 1687
-
Use of statistics for international comparisons, e.g., London vs. Rome and London vs. Paris, compared in people, housing, hospitals, etc.- William Petty (1623-1687), England [231,232].
PIC: Petty portrait (137 x 194; 3K)
- 1693
-
First real mortality tables, containing the ages at death of a stable sample of individuals under stable conditions
(from Breslau Bills of Mortality)- Edmond Halley (1656-1742), England [119].
TXT: Matthias Bohne edit of Halley 1693 paper
- 1693
-
First use of areas of rectangles to display probabilities of independent binary events- Edmond Halley (1656-1742), England [119].
IMG: Halley's diagram (356 x 237; 1K)
FIG: Halley 1893 2D diagram (284 x 232; 9.4K)
FIG: Halley 1893 3D diagram (461 x 450; 32K)